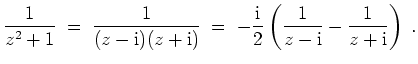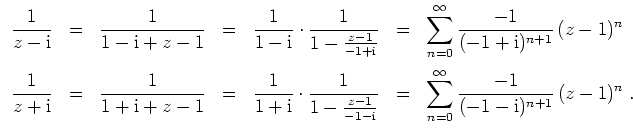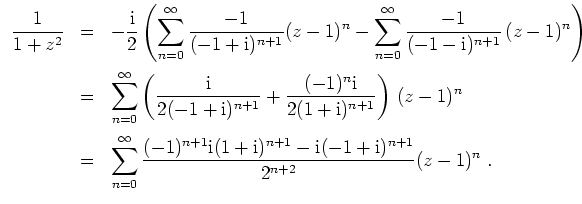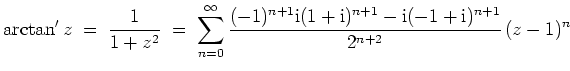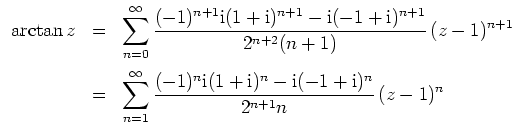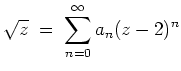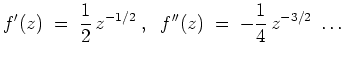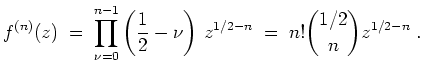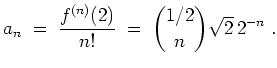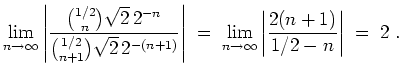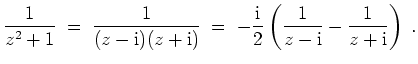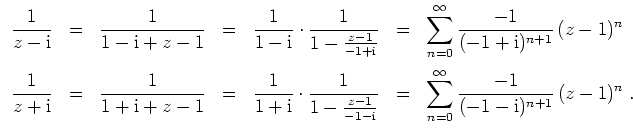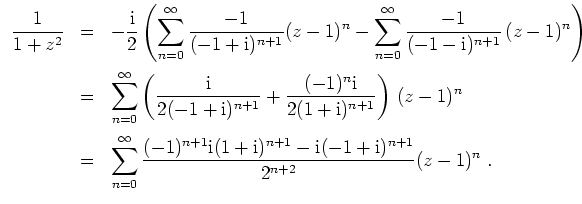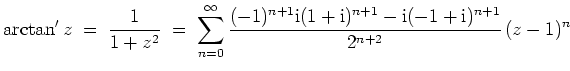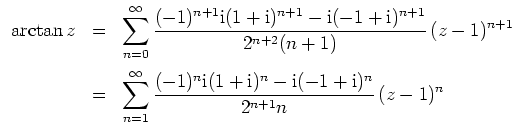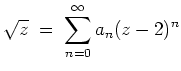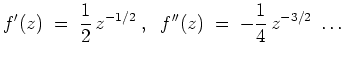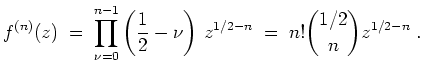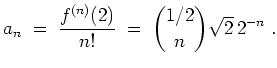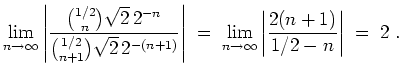Lösung.

  1. Mit Partialbruchzerlegung erhalten wir
    $ \mbox{$\displaystyle \dfrac{1}{z^2+1}\;=\; \dfrac{1}{(z-\text{i})(z+ \text{i}... ...\text{i}}{2}\left( \dfrac{1}{z-\text{i}} - \dfrac{1}{z+\text{i}} \right) \;. $}$
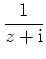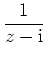    Wir wollen $ \mbox{$\dfrac{1}{z + \text{i}}$}$ und $ \mbox{$\dfrac{1}{z - \text{i}}$}$ mit der geometrischen Reihe in eine Potenzreihe entwickeln.

    Es wird

    $ \mbox{$\displaystyle \begin{array}{lclclcl} \dfrac{1}{z - \text{i}}&=& \dfrac... ...le\sum_{n=0}^\infty \dfrac{-1}{(-1-\text{i})^{n+1}}\, (z-1)^n \;. \end{array}$}$
    Insgesamt ergibt sich
    $ \mbox{$\displaystyle \begin{array}{rcl} \dfrac{1}{1+z^2} &=& -\dfrac{\text{i}... ...\text{i})^{n+1}-\text{i}(-1+\text{i})^{n+1}}{2^{n+2}} (z-1)^n \;. \end{array}$}$
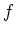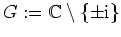    Die Funktion $ \mbox{$f$}$ ist holomorph auf dem Gebiet $ \mbox{$G:= \mathbb{C} \setminus \{\pm\text{i}\}$}$ . Also gilt für den Konvergenzradius
    $ \mbox{$\displaystyle R \;\ge \; d(1, \{\pm\text{i}\}) \;=\; \sqrt{2}\;. $}$
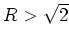    Es kann aber nicht $ \mbox{$R>\sqrt{2}$}$ gelten, denn sonst wäre 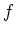$ \mbox{$f$}$ durch eine Potenzreihe dargestellt, welche im Punkt 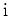$ \mbox{$\text{i}$}$ konvergiert, was der Nichtexistenz von 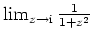$ \mbox{$\lim_{z \to \text{i}} \frac{1}{1+z^2}$}$ widerspräche. Also ist der Konvergenzradius
    $ \mbox{$\displaystyle R\;=\; \sqrt{2}\;. $}$

  2. Wir erinnern daran, daß
    $ \mbox{$\displaystyle \arctan : \mathbb{C}\setminus \{ \text{i}y \;\vert\; y \in \mathbb{R}, \vert y\vert\ge 1 \} \to \mathbb{C} $}$
    eine holomorphe Funktion ist. Es gilt nach 1.
    $ \mbox{$\displaystyle \arctan ' z\;=\; \dfrac {1}{1+z^2} \;=\; \sum_{n=0}^\in... ...1}\text{i}(1+\text{i})^{n+1}-\text{i}(-1+\text{i})^{n+1}}{2^{n+2}}\, (z-1)^n $}$
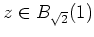    für $ \mbox{$z \in B_{\sqrt{2}}(1)$}$ . Daraus folgt
    $ \mbox{$\displaystyle \begin{array}{rcl} \arctan z &=& \displaystyle \sum_{n... ...(1+\text{i})^{n}-\text{i}(-1+\text{i})^{n}}{2^{n+1}n}\, (z-1)^{n} \end{array}$}$
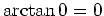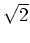    unter Beachtung von $ \mbox{$\arctan 0=0$}$ . Der Konvergenzradius beträgt wiederum $ \mbox{$\sqrt{2}$}$ .

  3. Wir erinnern daran, daß
    $ \mbox{$\displaystyle \mathbb{C}_- \to \mathbb{C}\;,\;\; z \mapsto \sqrt{z}\;=\; e^{\frac{1}{2}\,\text{Log }z} $}$
    eine holomorphe Funktion ist. Also besitzt sie eine Potenzreihendarstellung
    $ \mbox{$\displaystyle \sqrt{z}\;=\; \sum_{n=0}^\infty a_n (z-2)^n $}$
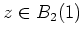    für $ \mbox{$z \in B_2(1)$}$ . Es gilt
    $ \mbox{$\displaystyle f'(z)\;=\; \dfrac{1}{2}\,z^{-1/2} \;,\;\; f''(z)\;=\; -\dfrac{1}{4}\,z^{-3/2}\;\ldots $}$
    Durch Induktion ergibt sich
    $ \mbox{$\displaystyle f^{(n)} (z)\;=\;\prod_{\nu=0}^{n-1}\left(\dfrac{1}{2}-\nu\right)\,z^{1/2-n}\;=\; n! {1/2 \choose n}z^{1/2-n}\;. $}$
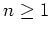    für $ \mbox{$n \ge 1$}$ . Daraus folgt
    $ \mbox{$\displaystyle a_n\;=\; \dfrac{f^{(n)}(2)}{n!}\;=\;{1/2 \choose n}\sqrt{2}\,2^{-n}\;. $}$
    Der Konvergenzradius ergibt sich zu
    $ \mbox{$\displaystyle \lim_{n \to \infty}\left\vert\dfrac {{1/2 \choose n}\sqr... ...\;=\;\lim_{n \to \infty}\left\vert\dfrac{2(n+1)}{1/2-n}\right\vert \;=\;2\;. $}$