Es sei
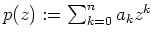 ein Polynom vom Grade
ein Polynom vom Grade
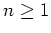 ohne Nullstellen in
ohne Nullstellen in
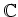 , und es sei
, und es sei
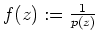 .
.
Es gilt
und
Also gibt es ein
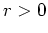 derart, daß
Daraus folgt
und damit
Da
derart, daß
Daraus folgt
und damit
Da
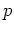 keine Nullstelle hat, ist
keine Nullstelle hat, ist
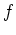 eine ganze Funktion. Wegen der Stetigkeit von
eine ganze Funktion. Wegen der Stetigkeit von
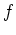 gibt es ein
gibt es ein
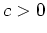 derart, daß
Also ist
derart, daß
Also ist
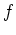 eine ganze beschränkte Funktion.
Nach dem Satz von Liouville folgt, daß
eine ganze beschränkte Funktion.
Nach dem Satz von Liouville folgt, daß
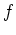 und damit auch
und damit auch
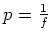 konstant ist.
konstant ist.
Da
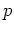 ein Polynom vom Grade
ein Polynom vom Grade
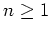 ist, ist dies ein Widerspruch.
ist, ist dies ein Widerspruch.
![]() ein Polynom vom Grade
ein Polynom vom Grade
![]() ohne Nullstellen in
ohne Nullstellen in
![]() , und es sei
, und es sei
![]() .
.
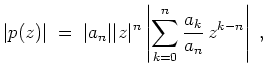
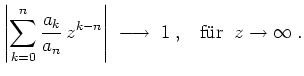
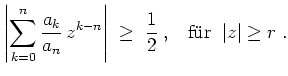
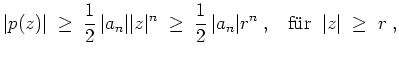
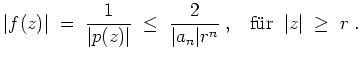
![]() ein Polynom vom Grade
ein Polynom vom Grade
![]() ist, ist dies ein Widerspruch.
ist, ist dies ein Widerspruch.