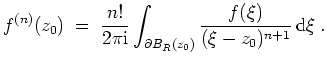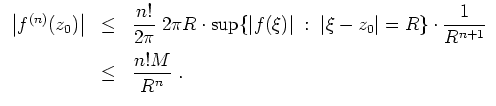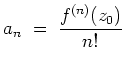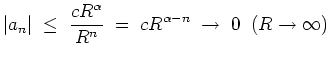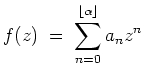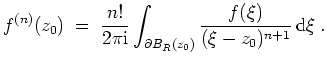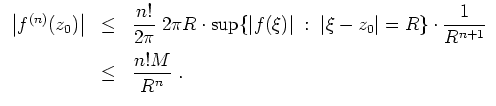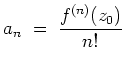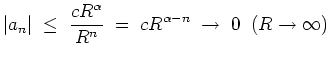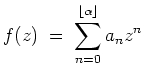- Wir betrachten die Cauchysche Integralformel für die
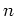 -te Ableitung
Mit der Standardabschätzung folgt
Mit der Gleichung
folgt die Behauptung.
-te Ableitung
Mit der Standardabschätzung folgt
Mit der Gleichung
folgt die Behauptung.
- Unter diesen Voraussetzungen gilt
für alle
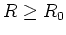 .
Mit dem 1. Teil der Aufgabe angewandt auf
.
Mit dem 1. Teil der Aufgabe angewandt auf
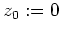 erhalten wir also
für
erhalten wir also
für
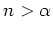 . Somit gilt
Die Potenzreihenentwicklung von
. Somit gilt
Die Potenzreihenentwicklung von
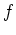 um
um
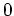 lautet daher
für alle
lautet daher
für alle
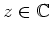 , d.h.
, d.h.
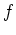 ist ein Polynom vom Grade
ist ein Polynom vom Grade
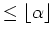 .
.