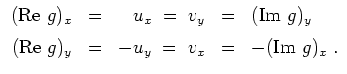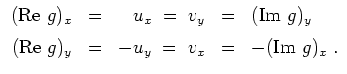- (i)
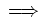 (ii):
(ii):
- Wir definieren
 durch
Aus den Cauchy-Riemannschen Differentialgleichungen folgt die Holomorphie von
durch
Aus den Cauchy-Riemannschen Differentialgleichungen folgt die Holomorphie von
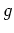 , denn setzt man
, denn setzt man
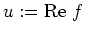 und
und
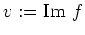 , so folgt
und
Ferner gilt für alle
, so folgt
und
Ferner gilt für alle
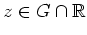 stets
stets
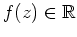 und daher
Da die Menge
und daher
Da die Menge
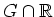 einen Häufungspunkt in
einen Häufungspunkt in
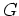 besitzt, folgt nach dem Identitätssatz für
holomorphe Funktionen, daß
für alle
besitzt, folgt nach dem Identitätssatz für
holomorphe Funktionen, daß
für alle
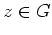 . Daraus folgt die Behauptung.
. Daraus folgt die Behauptung.
- (ii)
 (i):
(i):
- Für alle
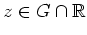 gilt
und daraus folgt
gilt
und daraus folgt
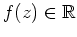 .
.