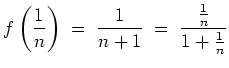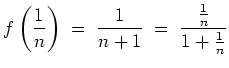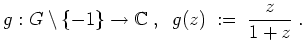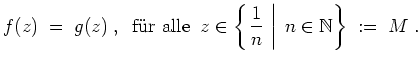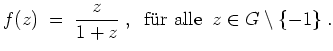Wir nehmen an, es gälte
für alle
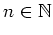 und wollen einen Widerspruch herleiten.
Wir definieren
Dann ist
und wollen einen Widerspruch herleiten.
Wir definieren
Dann ist
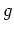 holomorph, und es gilt
Nun sind
holomorph, und es gilt
Nun sind
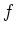 und
und
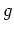 holomorph auf dem Gebiet
holomorph auf dem Gebiet
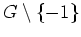 und stimmen auf der Menge
und stimmen auf der Menge
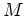 überein, welche den
Häufungspunkt
überein, welche den
Häufungspunkt
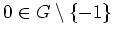 besitzt. Nach dem Identitätssatz folgt
Demnach hätte aber
besitzt. Nach dem Identitätssatz folgt
Demnach hätte aber
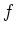 einen einfachen Pol im Punkt
einen einfachen Pol im Punkt
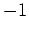 , im Widerspruch zur Holomorphie von
, im Widerspruch zur Holomorphie von
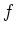 auf
auf
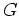 .
.