Zeige.
- (i)
- Schätze den Summanden auf jedem Kompaktum durch
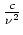 mit einer Konstanten
mit einer Konstanten
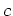 ab.
ab.
- (ii)
- Die Funktion
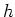 ist holomorph auf
ist holomorph auf
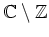 . Zeige mit Hilfe des Riemannschen Hebbarkeitssatzes,
daß
. Zeige mit Hilfe des Riemannschen Hebbarkeitssatzes,
daß
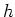 in den Punkten
in den Punkten
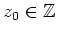 holomorph fortgestetzt werden kann.
holomorph fortgestetzt werden kann.
- (iii)
- Definiere
und zeige, daß
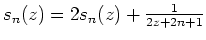 .
.
- (iv)
- Nach dem Maximumprinzip nimmt
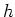 sein Maximum auf
sein Maximum auf
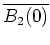 in einem
in einem
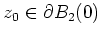 an.
Betrachte nun
an.
Betrachte nun
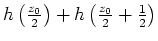 .
.
- (v)
- Die Funktion
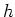 ist ungerade.
ist ungerade.
- Leite die Identität aus 1. ab.
- Setze in 2.
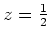 .
.
- Summiere getrennt über die geraden und ungeraden
 .
.
- Leite die Identität aus 2. zweimal ab.
- Analog zu 4.
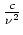 mit einer Konstanten
mit einer Konstanten
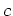 ab.
ab.
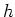 ist holomorph auf
ist holomorph auf
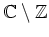 . Zeige mit Hilfe des Riemannschen Hebbarkeitssatzes,
daß
. Zeige mit Hilfe des Riemannschen Hebbarkeitssatzes,
daß
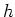 in den Punkten
in den Punkten
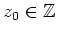 holomorph fortgestetzt werden kann.
holomorph fortgestetzt werden kann.
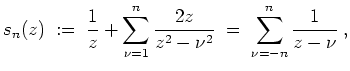
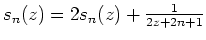 .
.
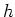 sein Maximum auf
sein Maximum auf
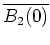 in einem
in einem
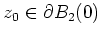 an.
Betrachte nun
an.
Betrachte nun
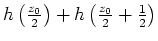 .
.
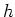 ist ungerade.
ist ungerade.