Zunächst ist klar, daß jede Möbiustransformation, welche
![]() auf sich abbildet, eine konforme Abbildung
auf sich abbildet, eine konforme Abbildung
![]() definiert.
definiert.
Es sei nun
![]() gegeben. Die Möbiustransformation
gegeben. Die Möbiustransformation
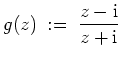
Also ist
![]() . Wie bekannt ist
. Wie bekannt ist
![]() daher eine Möbiustranformation.
Folglich ist auch
daher eine Möbiustranformation.
Folglich ist auch
![]() eine Möbiustransformation.
eine Möbiustransformation.