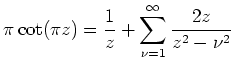 für alle
für alle
- (i)
- Die obige Funktionenreihe konvergiert normal in
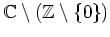 .
.
- (ii)
- Die Funktion
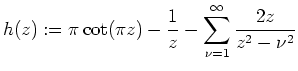 ist eine ganze Funktion.
ist eine ganze Funktion.
- (iii)
- Es gilt
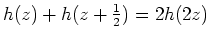 für alle
für alle
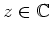 .
.
- (iv)
- Die Funktion
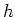 ist konstant.
ist konstant.
- (v)
- Die Funktion
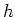 ist identisch
ist identisch
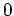 .
.
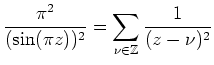 für alle
für alle
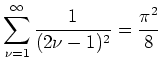 .
.
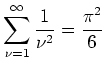 .
.
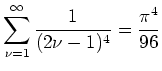 .
.
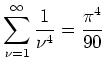 .
.