Repetitorium Funktionentheorie

Konforme Abbildungen und das Maximumprinzip.

Gebietstreue.

Es sei $\mbox{$G\subseteq\mathbb{C}$}$ , und $\mbox{$f:G\to\mathbb{C}$}$ sei eine holomorphe Funktion. Ist $\mbox{$f$}$ nicht konstant, so besagt der Satz von der Gebietstreue, daß $\mbox{$f(G)$}$ wiederum ein Gebiet ist.

Bemerkung: Der Zusammenhang von $\mbox{$f(G)$}$ folgt allein aus dem Zusammenhang von $\mbox{$G$}$ und der Stetigkeit von $\mbox{$f$}$ . Hingegen ist die Holomorphie und Inkonstanz von $\mbox{$f$}$ wesentlich für die Offenheit von $\mbox{$f(G)$}$ .

Konforme Abbildungen.

Eine bijektive holomorphe Funktion $\mbox{$f:G\to H$}$ heißt auch eine konforme Abbildung. In diesem Fall ist $\mbox{$g^{-1}:H\to G$}$ ebenfalls eine konforme Abbildung, und es gilt $\mbox{$f'(z)\ne 0$}$ für alle $\mbox{$z\in G$}$ .

Ist $\mbox{$G\subseteq\mathbb{C}$}$ ein Gebiet, so bildet die Menge

$\mbox{$\displaystyle A(G) \;:=\; \{f:G\to G\;\vert\; f \;\text{konform}\} $}$

eine Gruppe bezüglich der Komposition von Abbildungen, d.h. es gilt

$\mbox{$f,g\in A(G)\implies f\circ g\in A(G)$}$ .
$\mbox{$f\in A(G)\implies f^{-1}\in A(G)$}$ .
$\mbox{$\text{id}_G\in A(G)$}$ .

Maximumprinzip.

Es sei $\mbox{$G\subseteq\mathbb{C}$}$ ein Gebiet, und $\mbox{$f:G\to\mathbb{C}$}$ sei eine holomorphe Funktion.

Die erste Version des Maximumprinzips besagt, daß $\mbox{$\vert f\vert$}$ kein Maximum auf $\mbox{$G$}$ annimmt, sofern $\mbox{$f$}$ nicht konstant ist.

Die zweite Version des Maximumprinzips besagt, falls $\mbox{$G$}$ beschränkt ist und $\mbox{$f$}$ zusätzlich stetig auf $\mbox{$\overline{G}$}$ ist, so wird das Maximum von $\mbox{$\vert f\vert$}$ auf $\mbox{$\overline{G}$}$ auf dem Rand von $\mbox{$G$}$ angenommen.

Schwarzsches Lemma.

Es sei $\mbox{$\mathbb{E}:=\{z\in\mathbb{C}\;\vert\; \vert z\vert<1\}$}$ , und $\mbox{$f:\mathbb{E}\to\mathbb{C}$}$ sei holomorph mit

$\mbox{$\displaystyle f(0)\;=\;0\;,\;\; \vert f(z)\vert\;\le\;1\;,\;\;\text{f\uml ur alle}\;\; z\in\mathbb{E}\;. $}$

Dann gilt $\mbox{$\vert f'(0)\vert\le 1$}$ und $\mbox{$\vert f(z)\vert\le\vert z\vert$}$ für alle $\mbox{$z\in\mathbb{E}$}$ . Ferner tritt genau einer der beiden folgenden Fälle ein.

$\mbox{$\vert f'(0)\vert<1$}$ und $\mbox{$\vert f(z)\vert<\vert z\vert$}$ für alle $\mbox{$z\in\mathbb{E}\setminus\{0\}$}$ .
$\mbox{$\vert f'(0)\vert=1$}$ und es gibt ein $\mbox{$\alpha\in[0,2\pi)$}$ mit $\mbox{$f(z)=e^{\text{i}\alpha}$}$ für alle $\mbox{$z\in\mathbb{E}$}$ .

Mit Hilfe des Schwarzschen Lemmas lassen sich die konformen Abbildungen des Einheitskreises $\mbox{$\mathbb{E}$}$ bestimmen. Es gilt

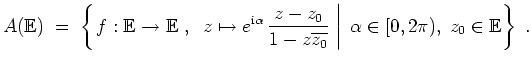
$\mbox{$\displaystyle A(\mathbb{E}) \;=\; \left\{\left.f:\mathbb{E}\to\mathbb{... ...rline{z_0}}\;\right\vert\; \alpha\in[0,2\pi),\; z_0\in\mathbb{E}\right\}\;. $}$

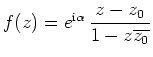In dieser Darstellung $\mbox{$f(z)=e^{\text{i}\alpha}\,\dfrac{z-z_0}{1-z\overline{z_0}}$}$ sind $\mbox{$z_0$}$ und $\mbox{$\alpha$}$ eindeutig durch $\mbox{$f$}$ bestimmt. Die konformen Abbildungen des Einheitskreises sind also genau die Möbiustransformationen, welche $\mbox{$\mathbb{E}$}$ auf sich abbilden.