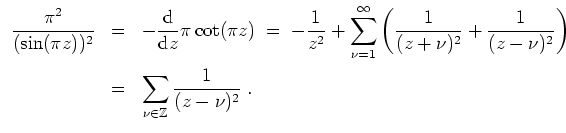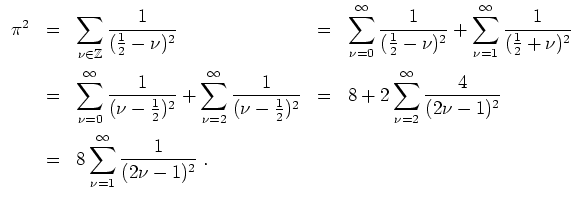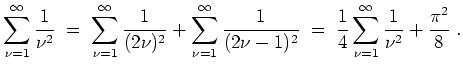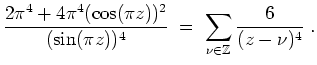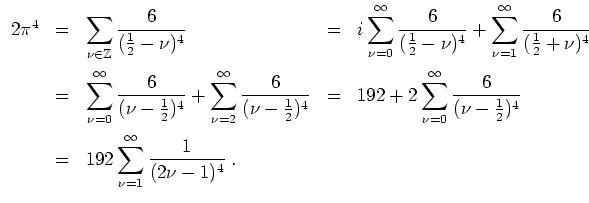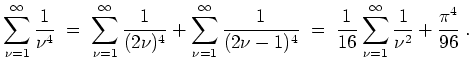- (i)
- Es sei
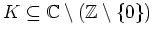 kompakt. Es sei
Für
kompakt. Es sei
Für
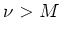 und
und
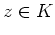 gilt dann
und
Daher erfüllt die Funktionenreihe auf
gilt dann
und
Daher erfüllt die Funktionenreihe auf
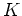 den Weierstraßschen
den Weierstraßschen
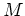 -Test, und sie konvergiert normal auf
-Test, und sie konvergiert normal auf
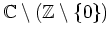 .
.
- (ii)
- Nach 1. ist
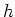 eine meromorphe Funktion mit Singularitäten in
eine meromorphe Funktion mit Singularitäten in
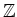 . Nun gilt aber
für alle
. Nun gilt aber
für alle
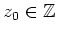 . Andererseits folgt auch
für alle
. Andererseits folgt auch
für alle
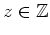 . Daher ist
für alle
. Daher ist
für alle
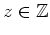 . Nach dem Riemannschen Hebbarkeitssatz sind alle Singularitäten von
. Nach dem Riemannschen Hebbarkeitssatz sind alle Singularitäten von
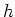 hebbar,
d.h. sie ist eine ganze Funktion.
hebbar,
d.h. sie ist eine ganze Funktion.
- (iii)
- Es sei zunächst
Dann folgt
Setzt man
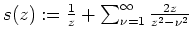 , so gilt nach obiger Identität durch
Grenzübergang
, so gilt nach obiger Identität durch
Grenzübergang
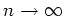 , daß
Nun erfüllt
, daß
Nun erfüllt
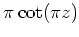 dieselbe Identität, wie man leicht nachrechnet. Daraus folgt mit Hilfe des Identitätssatzes
dieselbe Identität, wie man leicht nachrechnet. Daraus folgt mit Hilfe des Identitätssatzes
- (iv)
- Wir nehmen an,
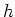 wäre nicht konstant. Nach dem Maximumprinzip gäbe es dann ein
wäre nicht konstant. Nach dem Maximumprinzip gäbe es dann ein
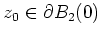 mit
Nach dem vorigen Aufgabenteil folgt dann aber
ein Widerspruch.
mit
Nach dem vorigen Aufgabenteil folgt dann aber
ein Widerspruch.
- (v)
- Die Funktion
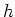 ist ungerade, da dies für alle Summanden in der Definition gilt. Ferner ist
ist ungerade, da dies für alle Summanden in der Definition gilt. Ferner ist
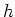 konstant. Daher ist
konstant. Daher ist
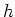 identisch
identisch
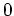 .
.
- Wegen
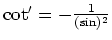 folgt durch Ableiten der Reihe in 1., daß
folgt durch Ableiten der Reihe in 1., daß
- Wir setzen in obige Darstellung von
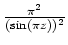 den Wert
den Wert
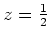 ein. Es wird
ein. Es wird
- Es wird
Durch Auflösen erhält man die Behauptung.
- Wir leiten die Formel aus 2. zweimal ab und erhalten
Speziell für
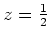 ergibt sich
ergibt sich
- Es wird
Durch Auflösen erhält man die Behauptung.
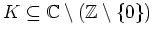 kompakt. Es sei
Für
kompakt. Es sei
Für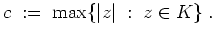
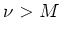 und
und
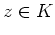 gilt dann
und
gilt dann
und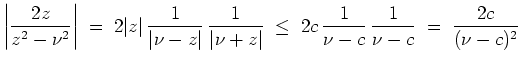 Daher erfüllt die Funktionenreihe auf
Daher erfüllt die Funktionenreihe auf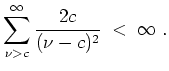
 den Weierstraßschen
den Weierstraßschen
 -Test, und sie konvergiert normal auf
-Test, und sie konvergiert normal auf
 .
.
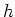 eine meromorphe Funktion mit Singularitäten in
eine meromorphe Funktion mit Singularitäten in
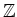 . Nun gilt aber
für alle
. Nun gilt aber
für alle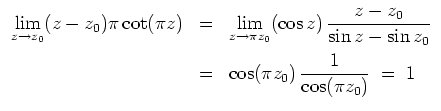
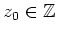 . Andererseits folgt auch
für alle
. Andererseits folgt auch
für alle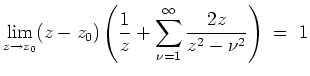
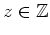 . Daher ist
für alle
. Daher ist
für alle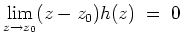
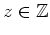 . Nach dem Riemannschen Hebbarkeitssatz sind alle Singularitäten von
. Nach dem Riemannschen Hebbarkeitssatz sind alle Singularitäten von
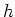 hebbar,
d.h. sie ist eine ganze Funktion.
hebbar,
d.h. sie ist eine ganze Funktion.
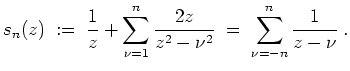 Setzt man
Setzt man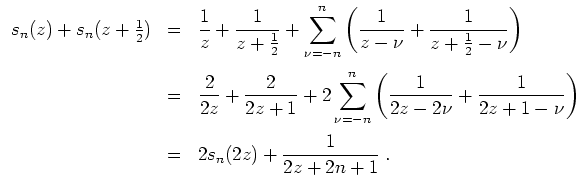
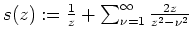 , so gilt nach obiger Identität durch
Grenzübergang
, so gilt nach obiger Identität durch
Grenzübergang
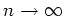 , daß
Nun erfüllt
, daß
Nun erfüllt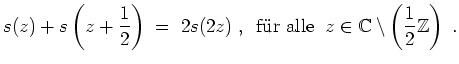
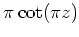 dieselbe Identität, wie man leicht nachrechnet. Daraus folgt mit Hilfe des Identitätssatzes
dieselbe Identität, wie man leicht nachrechnet. Daraus folgt mit Hilfe des Identitätssatzes
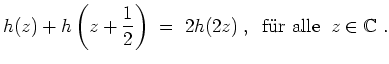
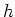 wäre nicht konstant. Nach dem Maximumprinzip gäbe es dann ein
wäre nicht konstant. Nach dem Maximumprinzip gäbe es dann ein
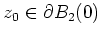 mit
Nach dem vorigen Aufgabenteil folgt dann aber
mit
Nach dem vorigen Aufgabenteil folgt dann aber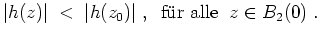 ein Widerspruch.
ein Widerspruch.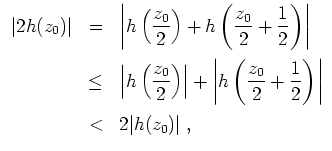
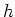 ist ungerade, da dies für alle Summanden in der Definition gilt. Ferner ist
ist ungerade, da dies für alle Summanden in der Definition gilt. Ferner ist
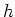 konstant. Daher ist
konstant. Daher ist
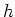 identisch
identisch
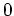 .
.