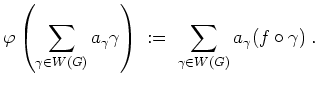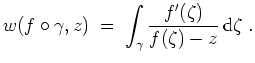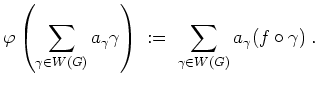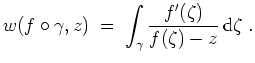- Beachte
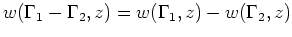 für alle
für alle
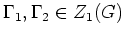 und alle
und alle
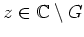 .
.
- Das Gebiet
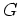 ist einfach zusammenhängend genau dann, wenn
ist einfach zusammenhängend genau dann, wenn
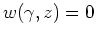 gilt für alle
gilt für alle
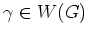 und alle
und alle
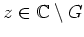 .
.
- Definiere einen Isomorphismus
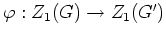 durch
Zeige
und verwende die Homologieversion des Cauchyschen Integralsatzes.
durch
Zeige
und verwende die Homologieversion des Cauchyschen Integralsatzes.
- Betrachte die Abbildung
- Die Gruppen
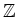 und
und
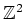 sind nicht isomorph.
sind nicht isomorph.