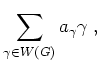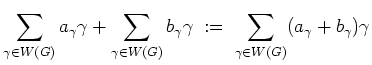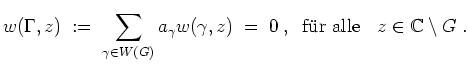(Die Homologiegruppe eines Gebiets)
Diese Aufgabe setzt elementare Kenntnisse in der Gruppentheorie voraus.
Es sei
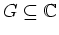 ein Gebiet, und es sei
ein Gebiet, und es sei
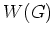 die Menge aller geschlossenen Wege in
die Menge aller geschlossenen Wege in
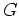 . Für diese
Aufgabe sei ein Wegezyklus eine formale Summe der Form
. Für diese
Aufgabe sei ein Wegezyklus eine formale Summe der Form
wobei
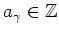 , und es gelte
, und es gelte
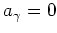 für fast alle
für fast alle
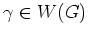 .
Es sei
.
Es sei
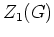 die Menge aller Wegezyklen in
die Menge aller Wegezyklen in
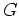 ; diese wird durch die Addition
zu einer abelschen Gruppe.
Ein Wegezyklus
; diese wird durch die Addition
zu einer abelschen Gruppe.
Ein Wegezyklus
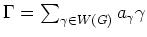 heißt
heißt
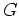 -nullhomolog, falls
Zeige.
-nullhomolog, falls
Zeige.
- Die Menge
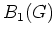 aller
aller
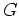 -nullhomologer Wegezyklen ist eine Untergruppe von
-nullhomologer Wegezyklen ist eine Untergruppe von
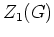 .
.
-
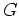 ist einfach zusammenhängend genau dann, wenn die Homologiegruppe von
ist einfach zusammenhängend genau dann, wenn die Homologiegruppe von
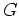 , definiert durch
, definiert durch
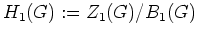 , trivial ist.
, trivial ist.
- Ist
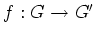 eine konforme Abbildung, so sind
eine konforme Abbildung, so sind
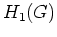 und
und
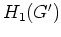 isomorph.
isomorph.
- Es sei
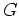 einfach zusammenhängend, und
einfach zusammenhängend, und
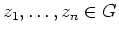 seien paarweise verschieden.
Dann ist
seien paarweise verschieden.
Dann ist
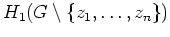 isomorph zu
isomorph zu
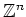 .
.
- Es gibt keine konforme Abbildung
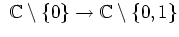 .
.
![]() ein Gebiet, und es sei
ein Gebiet, und es sei
![]() die Menge aller geschlossenen Wege in
die Menge aller geschlossenen Wege in
![]() . Für diese
Aufgabe sei ein Wegezyklus eine formale Summe der Form
. Für diese
Aufgabe sei ein Wegezyklus eine formale Summe der Form