Windungszahl.

Definition der Windungszahl.

Es sei $ \mbox{$\gamma:[a,b]\to\mathbb{C}$}$ ein geschlossener Weg, und es sei $ \mbox{$z\in\mathbb{C}$}$ mit $ \mbox{$z\ne\mathcal{T}(\gamma)$}$ . Dann definieren wir die Windungszahl oder Umlaufzahl von $ \mbox{$\gamma$}$ bezüglich $ \mbox{$z$}$ durch

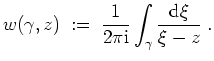
$ \mbox{$\displaystyle w(\gamma,z) \;:=\; \frac{1}{2\pi\text{i}}\int_\gamma \frac{\text{d}\xi}{\xi-z}\;. $}$
Das Innere von $ \mbox{$\gamma$}$ ist definiert durch
$ \mbox{$\displaystyle \text{Int}(\gamma) \;:=\; \{z\in\mathbb{C}\setminus\mathcal{T}(\gamma)\;\vert\; w(\gamma,z)\ne 0\}\;. $}$

Eigenschaften der Windungszahl:

Geometrische Bedeutung der Windungszahl.

Auf der oberen Halbebene $ \mbox{$\mathbb{H}:=\{z\in\mathbb{C}\;\vert\; \text{Im }z>0\}$}$ können wir den Winkel, den zwei Punkte $ \mbox{$z_1,z_2\in\mathbb{H}$}$ mit dem Nullpunkt einschließen, durch die Formel

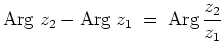
$ \mbox{$\displaystyle \text{Arg }z_2-\text{Arg }z_1 \;=\; \text{Arg}\,\frac{z_2}{z_1} $}$
messen.

Ist allgemeiner $ \mbox{$G=\left\{z\in\mathbb{C}\;\vert\; \text{Im}\,\frac{z-z_0}{w}>0\right\}$}$ die Halbebene ,,oberhalb`` der Geraden durch $ \mbox{$z_0$}$ in Richtung $ \mbox{$w$}$ , $ \mbox{$\vert w\vert=1$}$ , so ist

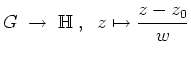
$ \mbox{$\displaystyle G\;\to\; \mathbb{H}\;,\;\; z\mapsto \frac{z-z_0}{w} $}$
eine holomorphe bijektive Abbildung, und der Winkel, den zwei Punkte $ \mbox{$z_1,z_2\in G$}$ mit $ \mbox{$z_0$}$ einschließen, kann durch die Formel
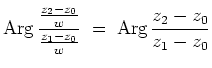
$ \mbox{$\displaystyle \text{Arg}\,\frac{\frac{z_2-z_0}{w}}{\frac{z_1-z_0}{w}} \;=\; \text{Arg}\,\frac{z_2-z_0}{z_1-z_0} $}$
bestimmt werden.

Es sei nun $ \mbox{$\gamma:[a,b]\to\mathbb{C}$}$ ein geschlossener Weg, und es sei $ \mbox{$z_0\in\mathbb{C}\setminus\mathcal{T}(\gamma)$}$ . Dann kann man eine Unterteilung $ \mbox{$a=t_0<t_1<\ldots<t_n=b$}$ wählen derart, daß die Teilkurven $ \mbox{$\gamma_{[t_k,t_{k+1}]}$}$ in Halbebenen bezüglich Geraden durch $ \mbox{$z_0$}$ liegen, d.h. es gibt Richtungen $ \mbox{$w_0,\ldots,w_{n-1}$}$ mit

$ \mbox{$\displaystyle \gamma([t_k,t_{k+1}]) \;\subseteq\; \left\{z\in\mathbb{C}\;\vert\; \text{Im}\,\frac{z-z_0}{w_k}>0\right\}\;=:\; G_k\;. $}$
Auf dem Gebiet $ \mbox{$G_k$}$ ist dann $ \mbox{$\text{Log}\,\frac{\xi-z_0}{w_k}$}$ eine Stammfunktion von $ \mbox{$\frac{1}{\xi-z_0}$}$ . Also ergibt sich für die Windungszahl
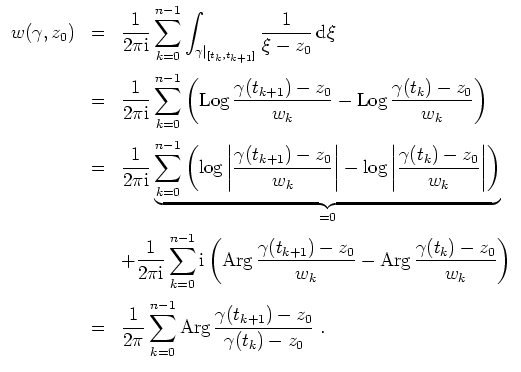
$ \mbox{$\displaystyle \begin{array}{rcl} w(\gamma,z_0) &=& \dfrac{1}{2\pi\text... ...^{n-1}\text{Arg}\,\dfrac{\gamma(t_{k+1})-z_0}{\gamma(t_k)-z_0}\;. \end{array}$}$
Somit zählt die Windungszahl gerade das $ \mbox{$\frac{1}{2\pi}$}$ -fache der aufsummierten Winkeländerungen von $ \mbox{$\gamma$}$ entlang der Unterteilung $ \mbox{$\gamma(t_0),\ldots,\gamma(t_n)$}$ . Dies entspricht der Anzahl der Windungen von $ \mbox{$\gamma$}$ um $ \mbox{$z_0$}$ , wobei Windungen im mathematisch negativen Sinne negativ gezählt werden.

Skizze einer Kurve $ \mbox{$\gamma$}$ mit $ \mbox{$w(\gamma,z_0)=2$}$ .

\includegraphics[width=10cm]{windung.eps}

Homologieversion des Cauchyschen Integralsatzes und der Cauchyschen Integralformel.

Es sei $ \mbox{$G\subseteq \mathbb{C}$}$ ein Gebiet, und $ \mbox{$\gamma_1, \ldots, \gamma_n$}$ seien geschlossene Wege in $ \mbox{$G$}$ . Dann heißt das Tupel $ \mbox{$\gamma := (\gamma_1, \ldots, \gamma_n)$}$ ein Wegezyklus in $ \mbox{$G$}$ . Wir definieren die Windungszahl von $ \mbox{$\gamma$}$ bezüglich $ \mbox{$z \in \mathbb{C} \setminus \mathcal{T}(\gamma)$}$ durch

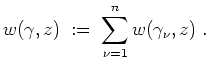
$ \mbox{$\displaystyle w(\gamma,z) \;:=\; \sum_{\nu=1}^n w(\gamma_{\nu},z)\;. $}$
Für eine holomorphe Funktion $ \mbox{$f:G \to \mathbb{C}$}$ setzen wir
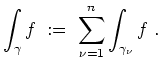
$ \mbox{$\displaystyle \int_{\gamma} f \;:=\; \sum_{\nu=1}^n \int_{\gamma_\nu} f\;. $}$
Der Wegezyklus $ \mbox{$\gamma$}$ heißt $ \mbox{$G$}$ -nullhomolog, falls
$ \mbox{$\displaystyle w(\gamma,z)\;=\;0\;,\;\; \text{f\uml ur alle }\;\; z\in \mathbb{C} \setminus G\;. $}$
Anschaulich bedeutet $ \mbox{$G$}$ -nullhomolog, daß der Wegezyklus keine Punkte des Komplements von $ \mbox{$G$}$ umläuft.

Es sei nun $ \mbox{$\gamma$}$ ein $ \mbox{$G$}$ -nullhomologer Wegezyklus und $ \mbox{$f:G \to \mathbb{C}$}$ eine holomorphe Funktion. Dann besagt die Homologieversion des Cauchyschen Integralsatzes, daß

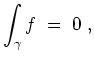
$ \mbox{$\displaystyle \int_\gamma f \;=\;0\;, $}$
und die Homologieversion der Cauchyschen Integralformel besagt, daß für alle $ \mbox{$z \in \mathbb{C} \setminus \mathcal{T}(\gamma)$}$ gilt
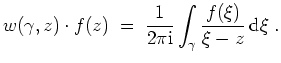
$ \mbox{$\displaystyle w(\gamma,z)\cdot f(z) \;=\; \frac{1}{2 \pi \text{i}} \int_\gamma \frac{f(\xi)}{\xi-z} \,\text{d} \xi\;. $}$

Homotopie.

Es sei $ \mbox{$G\subseteq \mathbb{C}$}$ ein Gebiet und es seien $ \mbox{$\alpha, \beta ;[a,b] \to G$}$ zwei Wege, die jeweils denselben Anfangspunkt $ \mbox{$z$}$ und denselben Endpunkt $ \mbox{$w$}$ haben. Eine Homotopie von $ \mbox{$\alpha$}$ nach $ \mbox{$\beta$}$ in G ist eine stetige Abbildung

$ \mbox{$\displaystyle H : [a,b]\times [0,1] \to G $}$
mit Die Kurve $ \mbox{$\alpha$}$ heißt dann $ \mbox{$G$}$ -homotop zur Kurve $ \mbox{$\beta$}$ .

Skizze von $ \mbox{$\alpha, H(.,\frac{1}{10}), \ldots H(.,\frac{9}{10}), \beta$}$ .

\includegraphics[width=8cm]{homotop.eps}

Ist $ \mbox{$\alpha$}$ ein geschlossener Weg und $ \mbox{$G$}$ -homotop zu einer konstanten Kurve, so heißt $ \mbox{$\alpha$}$ $ \mbox{$G$}$ -nullhomotop.

Es seien $ \mbox{$\alpha$}$ und $ \mbox{$\beta$}$ $ \mbox{$G$}$ -homotope Kurven und $ \mbox{$f:G \to \mathbb{C}$}$ sei holomorph. Dann besagt die Homotopieversion des Cauchyschen Integralsatzes, daß

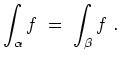
$ \mbox{$\displaystyle \int_\alpha f \;=\; \int_\beta f \;. $}$
Ist $ \mbox{$\alpha$}$ $ \mbox{$G$}$ -nullhomotop, so folgt
$ \mbox{$\displaystyle \int_\alpha f \;=\; 0\;. $}$

Insbesondere ist ein $ \mbox{$G$}$ -nullhomotoper Weg auch $ \mbox{$G$}$ -nullhomolog.

Charakterisierung einfach zusammenhängender Gebiete.

Ein Gebiet $ \mbox{$G\subseteq \mathbb{C}$}$ heißt einfach zusammenhängend, falls eine der folgenden äquivalenten Bedingungen erfüllt ist.

Die dritte Eigenschaft besagt, daß ein Weg in $ \mbox{$G$}$ keine Punkte des Komplementes von $ \mbox{$G$}$ umlaufen kann. Die vierte Eigenschaft besagt, daß ein Weg in $ \mbox{$G$}$ stetig auf einen Punkt zusammengezogen werden kann, ohne $ \mbox{$G$}$ zu verlassen.