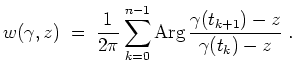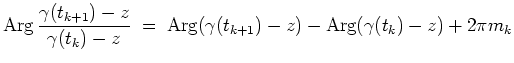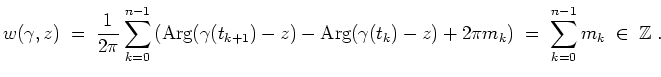Es sei etwa
![]() . Dann gibt es eine endliche Menge
. Dann gibt es eine endliche Menge
![]() derart, daß
derart, daß
![]() stetig
differenzierbar ist auf
stetig
differenzierbar ist auf
![]() . Man definiere
. Man definiere
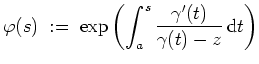
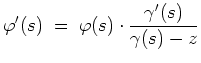
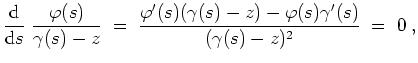
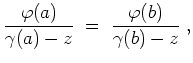
Alternativlösung:
Man wähle eine Unterteilung
![]() derart, daß die Teilkurven
derart, daß die Teilkurven
![]() in Halbebenen
bezüglich Geraden durch
in Halbebenen
bezüglich Geraden durch
![]() liegen.
Für die Windungszahl gilt dann
liegen.
Für die Windungszahl gilt dann