- Beweise durch Induktion nach
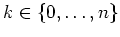 , daß gilt
, daß gilt
- Betrachte die Folge
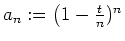 und zeige mit Bernoulli, daß
und zeige mit Bernoulli, daß
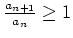 gilt.
gilt.
- Beweise zunächst, daß für
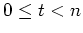 gilt, daß
Zeige damit, daß
gilt, daß
Zeige damit, daß
- Zeige, daß
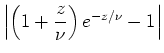 auf jedem Kompaktum durch
auf jedem Kompaktum durch
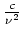 abgeschätzt werden kann mit einer Konstanten
abgeschätzt werden kann mit einer Konstanten
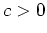 .
.
- Zeige, daß
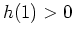 gilt.
gilt.
- Bestimme
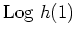 .
.
- Betrachte die Funktion
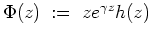 , und zeige mit 2., daß diese Funktion für
, und zeige mit 2., daß diese Funktion für
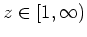 mit
mit
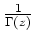 übereinstimmt.
übereinstimmt.
- Bestimme die Nullstellen der Funktion
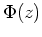 .
.
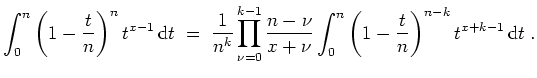
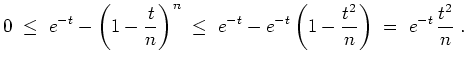
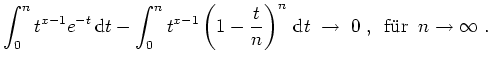
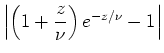 auf jedem Kompaktum durch
auf jedem Kompaktum durch
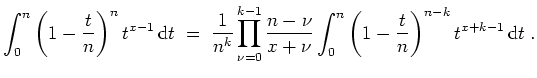
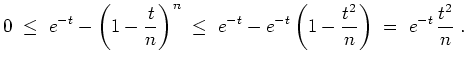
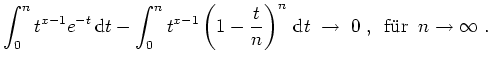
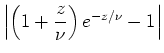 auf jedem Kompaktum durch
auf jedem Kompaktum durch