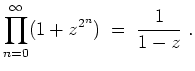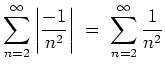
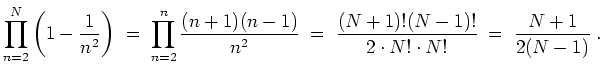
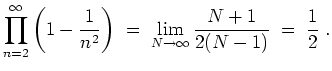
Es sei nun
![]() . Dann konvergiert das Produkt sogar absolut, denn die Reihe
. Dann konvergiert das Produkt sogar absolut, denn die Reihe
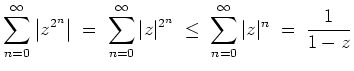
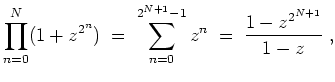
Das unendliche Proukt
![]() konvergiert also genau dann, wenn
konvergiert also genau dann, wenn
![]() , und dann konvergiert es auch absolut und
hat den Wert
, und dann konvergiert es auch absolut und
hat den Wert
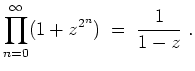
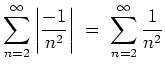
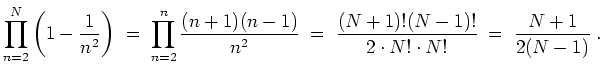
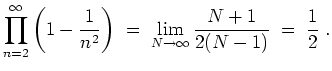
Es sei nun
![]() . Dann konvergiert das Produkt sogar absolut, denn die Reihe
. Dann konvergiert das Produkt sogar absolut, denn die Reihe
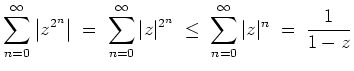
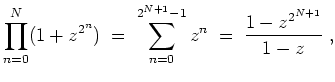
Das unendliche Proukt
![]() konvergiert also genau dann, wenn
konvergiert also genau dann, wenn
![]() , und dann konvergiert es auch absolut und
hat den Wert
, und dann konvergiert es auch absolut und
hat den Wert