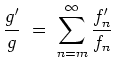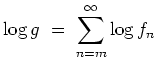Es sei
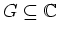 ein Gebiet, und
ein Gebiet, und
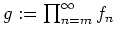 sei kompakt konvergent auf
sei kompakt konvergent auf
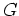 .
Ferner sei jede Funktion
.
Ferner sei jede Funktion
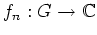 holomorph und nicht identisch
holomorph und nicht identisch
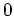 , und es sei
, und es sei
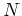 die Vereinigung der Nullstellenmengen aller Funktionen
die Vereinigung der Nullstellenmengen aller Funktionen
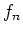 ,
,
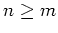 .
.
- Zeige, daß
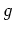 holomorph ist, und für die logarithmische Ableitung von
holomorph ist, und für die logarithmische Ableitung von
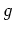 gilt, daß
auf
gilt, daß
auf
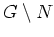 , und die Reihe konvergiert kompakt auf
, und die Reihe konvergiert kompakt auf
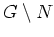 .
.
- Es sei nun
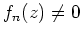 für alle
für alle
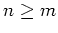 und alle
und alle
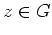 , d.h.
, d.h.
 . Ferner sei
. Ferner sei
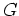 einfach zusammenhängend.
Zeige, daß es Zweige
einfach zusammenhängend.
Zeige, daß es Zweige
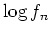 der Funktionen
der Funktionen
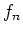 derart gibt, daß
auf
derart gibt, daß
auf
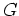 gilt, und die Reihe konvergiert kompakt auf
gilt, und die Reihe konvergiert kompakt auf
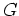 .
.
![]() ein Gebiet, und
ein Gebiet, und
![]() sei kompakt konvergent auf
sei kompakt konvergent auf
![]() .
Ferner sei jede Funktion
.
Ferner sei jede Funktion
![]() holomorph und nicht identisch
holomorph und nicht identisch
![]() , und es sei
, und es sei
![]() die Vereinigung der Nullstellenmengen aller Funktionen
die Vereinigung der Nullstellenmengen aller Funktionen
![]() ,
,
![]() .
.