Die Eulersche Gammafunktion.
Die Eulersche Gammafunktion ist eine auf
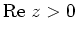 holomorphe Funktion, definiert durch
holomorphe Funktion, definiert durch
Ziel dieser Aufgabe ist die Darstellung von
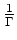 als ganze Funktion und von
als ganze Funktion und von
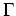 als meromorphe Funktion vermöge
für alle
als meromorphe Funktion vermöge
für alle
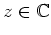 bzw. alle
bzw. alle
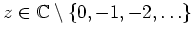 .
Zeige dazu die folgenden Schritte.
.
Zeige dazu die folgenden Schritte.
-
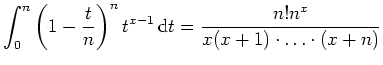 für
für
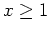 .
.
-
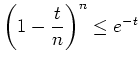 für alle
für alle
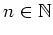 mit
mit
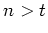 .
.
-
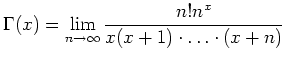 für alle
für alle
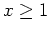 .
.
- Das unendliche Produkt
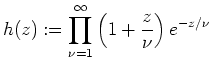 konvergiert normal auf
konvergiert normal auf
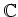 und stellt eine ganze Funktion dar.
und stellt eine ganze Funktion dar.
- Es gibt ein
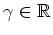 so, daß
so, daß
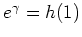 .
.
-
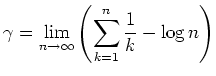 . (Eulersche Konstante)
. (Eulersche Konstante)
-
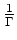 läßt sich zu einer ganzen Funktion fortsetzen, und es gilt obige Darstellung für
läßt sich zu einer ganzen Funktion fortsetzen, und es gilt obige Darstellung für
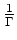 auf
auf
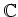 .
.
-
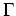 besitzt eine meromorphe Fortsetzung auf
besitzt eine meromorphe Fortsetzung auf
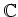 . Ihre Singularitäten sind Pole der Ordnung
. Ihre Singularitäten sind Pole der Ordnung
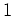 in den Punkten
in den Punkten
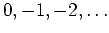 . Es gilt obige Darstellung für
. Es gilt obige Darstellung für
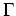 auf
auf
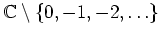 .
Ferner hat
.
Ferner hat
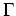 keine Nullstelle auf
keine Nullstelle auf
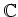 .
.
![]() holomorphe Funktion, definiert durch
holomorphe Funktion, definiert durch
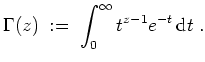
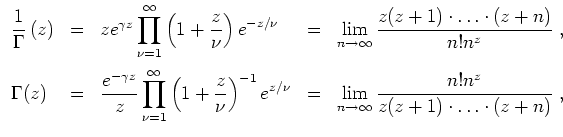
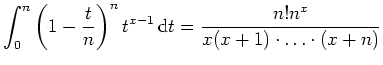 für
für
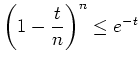 für alle
für alle
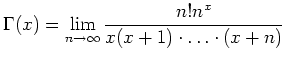 für alle
für alle
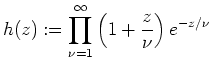 konvergiert normal auf
konvergiert normal auf
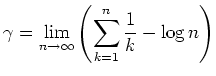 . (Eulersche Konstante)
. (Eulersche Konstante)