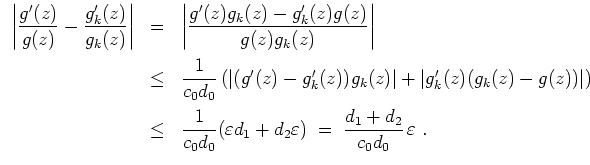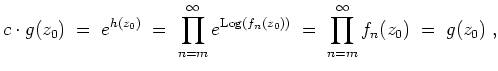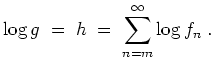Die Funktion
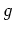 ist als Grenzfunktion einer kompakt konvergenten Funktionenfolge holomorph. Ferner ist
ist als Grenzfunktion einer kompakt konvergenten Funktionenfolge holomorph. Ferner ist
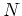 die Menge der Nullstellen
von
die Menge der Nullstellen
von
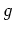 in
in
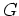 . Insbesondere hat
. Insbesondere hat
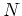 keinen Häufungspunkt in
keinen Häufungspunkt in
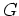 und
und
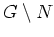 ist ein Gebiet.
ist ein Gebiet.
Es sei nun
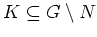 kompakt. Es sei
kompakt. Es sei
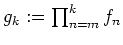 . Dann gilt
. Dann gilt
auf
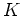 . Wir wollen zeigen, daß
. Wir wollen zeigen, daß
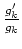 gleichmäßig auf
gleichmäßig auf
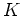 gegen
gegen
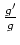 konvergiert.
konvergiert.
Zunächst gibt es Konstanten
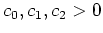 derart, daß
derart, daß
Es sei nun
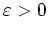 . Wegen der gleichmäßigen Konvergenz von
. Wegen der gleichmäßigen Konvergenz von
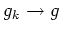 und
und
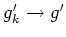 auf
auf
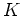 gibt es ein
gibt es ein
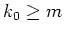 derart, daß für alle
derart, daß für alle
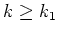 und alle
und alle
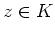 gilt, daß
Nimmt man zusätzlich
gilt, daß
Nimmt man zusätzlich
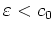 an, so gilt auch noch
für alle
an, so gilt auch noch
für alle
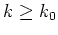 und alle
und alle
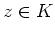 , und somit
Also konvergiert
, und somit
Also konvergiert
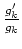 gleichmäßig auf
gleichmäßig auf
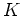 gegen
gegen
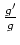 .
Da
.
Da
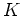 beliebig war, folgt die Behauptung.
beliebig war, folgt die Behauptung.
![]() kompakt. Es sei
kompakt. Es sei
![]() . Dann gilt
. Dann gilt
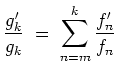
![]() derart, daß
derart, daß
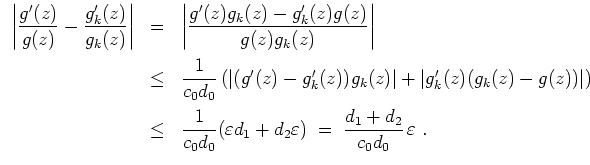
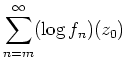
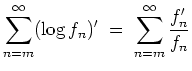
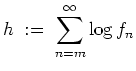
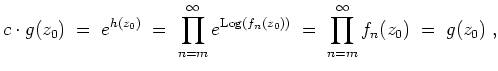
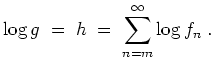
![]() kompakt. Es sei
kompakt. Es sei
![]() . Dann gilt
. Dann gilt
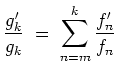
![]() derart, daß
derart, daß