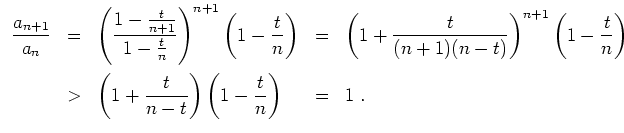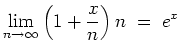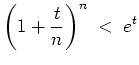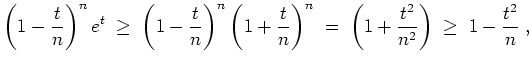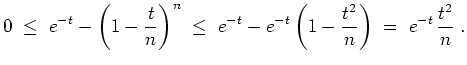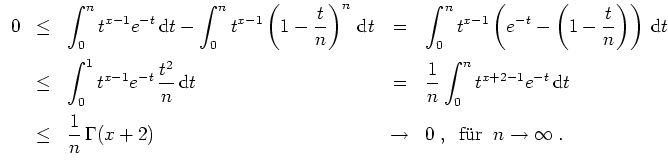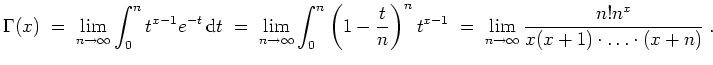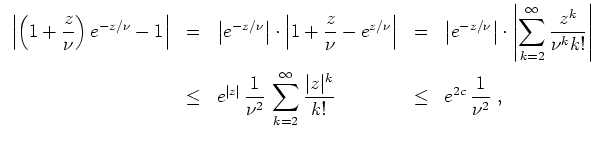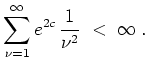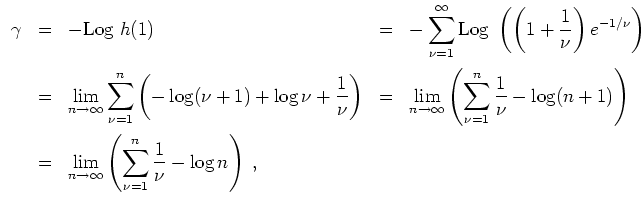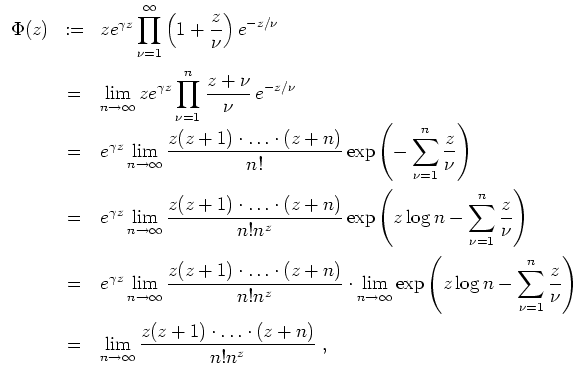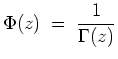- Wir zeigen durch Induktion nach
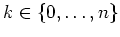 , daß
Für
, daß
Für
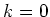 ist dies klar. Für den Induktionsschritt betrachte man die partielle Integration
Daraus folgt die obige Behautpung. Für
ist dies klar. Für den Induktionsschritt betrachte man die partielle Integration
Daraus folgt die obige Behautpung. Für
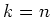 ergibt sich die geforderte Gleichung.
ergibt sich die geforderte Gleichung.
- Die Folge
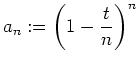 ist für
ist für
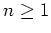 ,
,
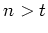 monoton wachsend, denn es gilt mit Hilfe der Bernoullischen
Ungleichung
Ferner ist bekannt, daß
für alle
monoton wachsend, denn es gilt mit Hilfe der Bernoullischen
Ungleichung
Ferner ist bekannt, daß
für alle
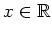 gilt. Daraus folgt die Behauptung.
gilt. Daraus folgt die Behauptung.
- Nach dem vorigem gilt auch
für
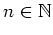 ,
,
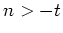 . Speziell gilt also für
. Speziell gilt also für
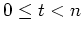 mit der Bernoullischen Ungleichung
und daher
Somit wird
Mit Aufgabenteil 2. folgt daher für alle
mit der Bernoullischen Ungleichung
und daher
Somit wird
Mit Aufgabenteil 2. folgt daher für alle
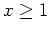 , daß
, daß
- Es sei
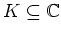 eine kompakte Teilmenge. Es sei
eine kompakte Teilmenge. Es sei
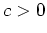 so gewählt, daß
so gewählt, daß
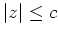 für alle
für alle
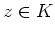 gilt.
Dann folgt für alle
gilt.
Dann folgt für alle
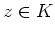 , daß
und
Somit konvergiert das unendliche Produkt normal auf
, daß
und
Somit konvergiert das unendliche Produkt normal auf
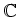 und stellt eine ganze Funktion dar.
und stellt eine ganze Funktion dar.
- Es gilt offenbar
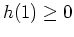 , und da das Produkt konvergiert, gilt auch
, und da das Produkt konvergiert, gilt auch
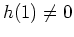 . Folglich gibt es ein solches
. Folglich gibt es ein solches
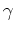 .
.
- Es gilt
denn es gilt
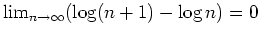 .
.
- Es gilt
denn
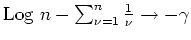 für
für
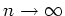 .
Mit Aufgabenteil 3. folgt
für alle
.
Mit Aufgabenteil 3. folgt
für alle
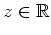 mit
mit
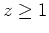 . Aufgrund des Identitätssatzes für holomorphe Funktionen ist
. Aufgrund des Identitätssatzes für holomorphe Funktionen ist
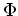 die eindeutig bestimmte holomorphe Fortsetzung von
die eindeutig bestimmte holomorphe Fortsetzung von
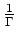 auf
auf
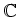 . Die Behauptung folgt.
. Die Behauptung folgt.
- Die ganze Funktion
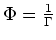 hat nach obiger Produktdarstellung lauter einfache Nullstellen in den Punkten
hat nach obiger Produktdarstellung lauter einfache Nullstellen in den Punkten
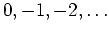 , und sie hat keine weiteren Nullstellen. Somit ist
, und sie hat keine weiteren Nullstellen. Somit ist
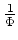 eine meromorphe Funktion, deren
Singularitäten jeweils einfache Pole in den Punkten
eine meromorphe Funktion, deren
Singularitäten jeweils einfache Pole in den Punkten
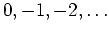 sind. Daher ist
sind. Daher ist
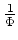 eine
meromorphe Fortsetzung von
eine
meromorphe Fortsetzung von
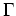 . Da
. Da
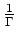 eine ganze Funktion ist, kann
eine ganze Funktion ist, kann
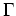 keine Nullstellen auf
keine Nullstellen auf
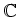 haben.
haben.
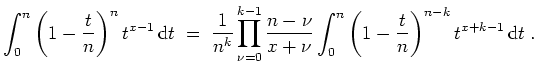
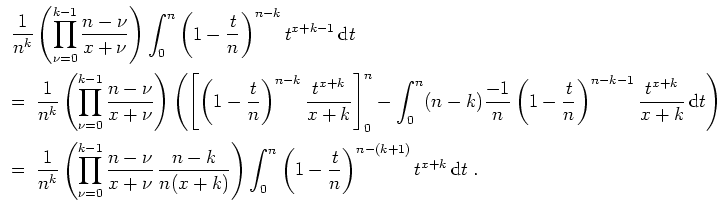
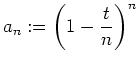 ist für
ist für
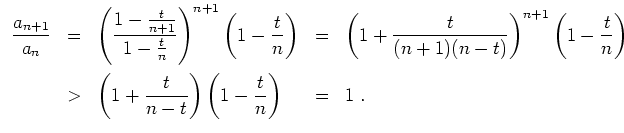
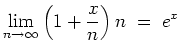
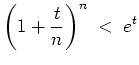
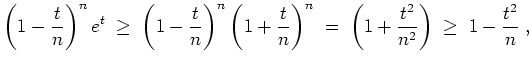
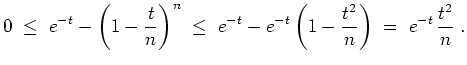
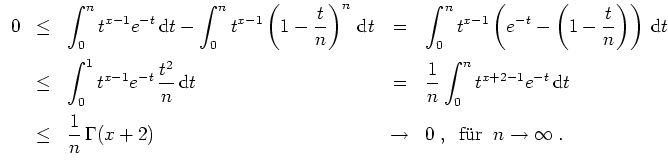
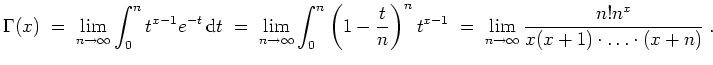
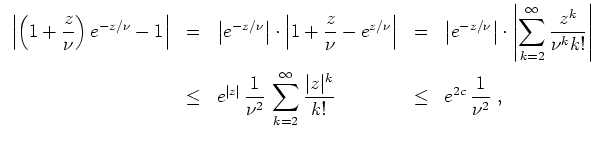
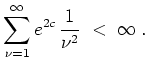
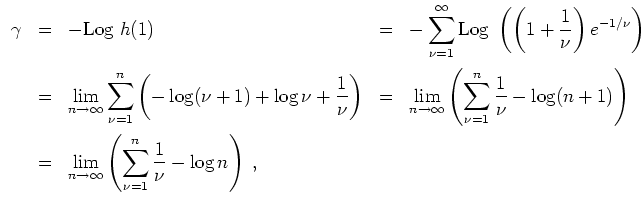
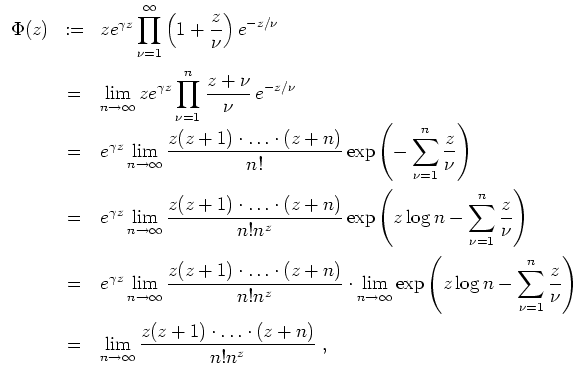
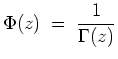
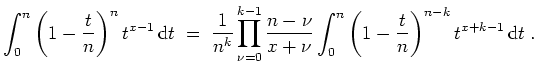
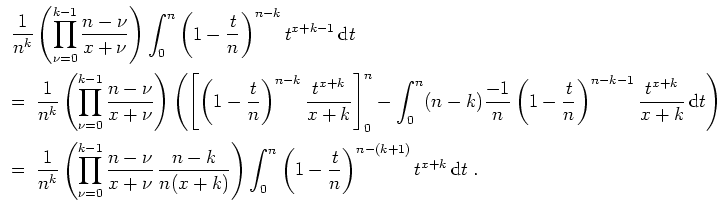
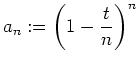 ist für
ist für