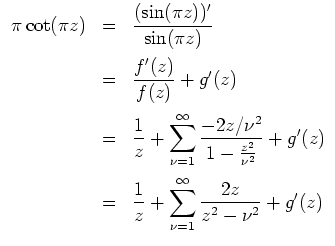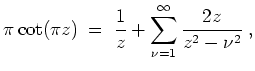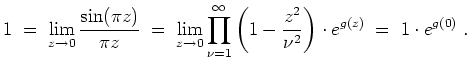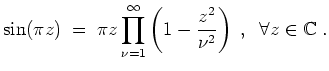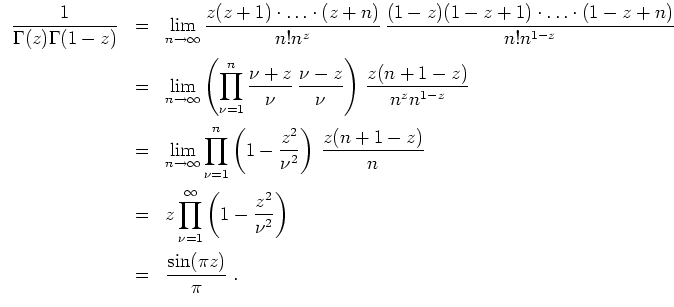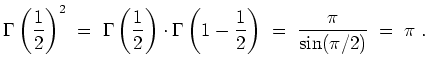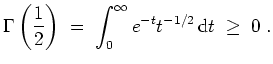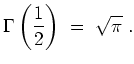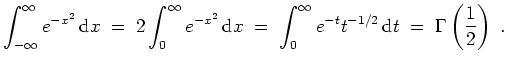Es sei
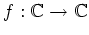 definiert durch
Das unendliche Produkt in dieser Definition ist normal konvergent auf
definiert durch
Das unendliche Produkt in dieser Definition ist normal konvergent auf
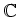 , denn auf jedem Kompaktum
, denn auf jedem Kompaktum
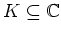 gilt
mit
gilt
mit
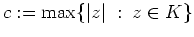 , und
, und
Folglich stellt
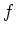 eine ganze Funktion dar, und sie besitzt nur einfache Nullstellen in den ganzen Zahlen.
Die Funktion
eine ganze Funktion dar, und sie besitzt nur einfache Nullstellen in den ganzen Zahlen.
Die Funktion
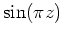 besitzt dieselben einfachen Nullstellen, somit ist
besitzt dieselben einfachen Nullstellen, somit ist
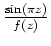 fortsetzbar
zu einer ganzen Funktion ohne Nullstelle.
Da
fortsetzbar
zu einer ganzen Funktion ohne Nullstelle.
Da
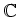 einfach zusammenhängend ist, gibt es einen Logarithmus
einfach zusammenhängend ist, gibt es einen Logarithmus
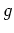 dieser Funktion, d.h. eine ganze Funktion
dieser Funktion, d.h. eine ganze Funktion
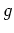 mit
mit
Betrachtet man die logarithmischen Ableitungen dieser Funktionen, so ergibt sich
für alle
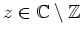 .
Vergleicht man das mit der bekannten Identität
so folgt daraus
.
Vergleicht man das mit der bekannten Identität
so folgt daraus
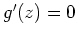 für alle
für alle
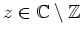 . Aus dem Identitätssatz für holomorphe Funktionen
folgt
. Aus dem Identitätssatz für holomorphe Funktionen
folgt
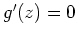 für alle
für alle
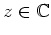 . Somit ist
. Somit ist
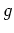 konstant.
Der Wert dieser Konstanten ergibt sich durch
Also ist
konstant.
Der Wert dieser Konstanten ergibt sich durch
Also ist
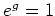 auf
auf
 , und es folgt die Produktdarstellung
, und es folgt die Produktdarstellung
Daraus ergibt sich auch der Zusammenhang mit der Gammafunktion:
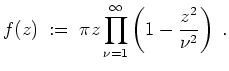
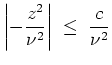
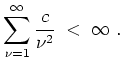
![]() eine ganze Funktion dar, und sie besitzt nur einfache Nullstellen in den ganzen Zahlen.
Die Funktion
eine ganze Funktion dar, und sie besitzt nur einfache Nullstellen in den ganzen Zahlen.
Die Funktion
![]() besitzt dieselben einfachen Nullstellen, somit ist
besitzt dieselben einfachen Nullstellen, somit ist
![]() fortsetzbar
zu einer ganzen Funktion ohne Nullstelle.
Da
fortsetzbar
zu einer ganzen Funktion ohne Nullstelle.
Da
![]() einfach zusammenhängend ist, gibt es einen Logarithmus
einfach zusammenhängend ist, gibt es einen Logarithmus
![]() dieser Funktion, d.h. eine ganze Funktion
dieser Funktion, d.h. eine ganze Funktion
![]() mit
mit