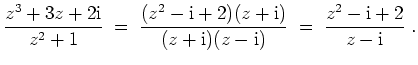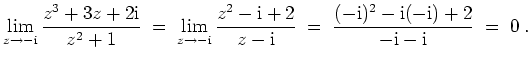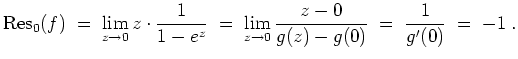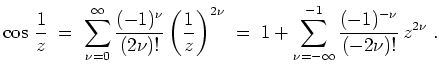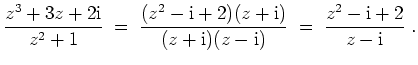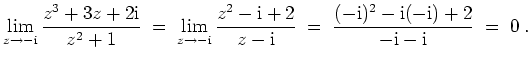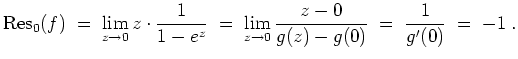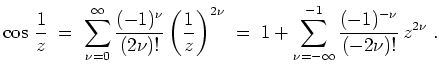- Durch Polynomdivision ergibt sich
Es handelt sich also um eine hebbare Singularität.
Der Grenzwert zum Punkt
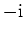 ist
ist
- Der Punkt
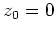 ist eine Nullstelle der Ordnung
ist eine Nullstelle der Ordnung
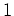 von
von
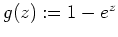 , denn es gilt
Daher ist
, denn es gilt
Daher ist
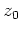 ein Pol der Ordnung
ein Pol der Ordnung
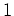 von
von
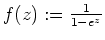 .
Das Residuum von
.
Das Residuum von
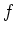 in
in
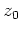 ergibt sich zu
Damit ergibt sich der Hauptteil zu
ergibt sich zu
Damit ergibt sich der Hauptteil zu
- Mit der Potenzreihenentwicklung von
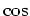 um
um
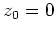 ergibt sich die Laurentreihenentwicklung
Der Hauptteil dieser Laurentreihe hat unendlich viele Koeffizienten
ergibt sich die Laurentreihenentwicklung
Der Hauptteil dieser Laurentreihe hat unendlich viele Koeffizienten
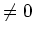 . Damit ist
. Damit ist
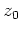 eine wesentliche Singularität von
eine wesentliche Singularität von
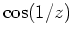 .
.