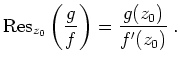Es sei
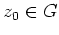 eine Singularität einer holomorphen Funktion
eine Singularität einer holomorphen Funktion
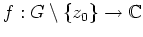 , und
es sei
, und
es sei
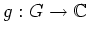 holomorph.
Zeige.
holomorph.
Zeige.
- Ist
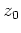 Pol der Ordnung 1 von
Pol der Ordnung 1 von
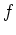 , so gilt
, so gilt
- Ist
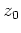 eine Nullstelle der Ordnung 1 von
eine Nullstelle der Ordnung 1 von
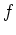 , so gilt
, so gilt
- Es sei
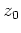 hebbar oder ein Pol und es sei
hebbar oder ein Pol und es sei
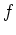 nicht identisch
nicht identisch
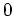 . Dann gilt
. Dann gilt
- Bestimme den Hauptteil der Laurentreihenentwicklung und das Residuum von
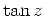 im Punkt
im Punkt
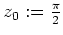 .
.
![]() eine Singularität einer holomorphen Funktion
eine Singularität einer holomorphen Funktion
![]() , und
es sei
, und
es sei
![]() holomorph.
Zeige.
holomorph.
Zeige.