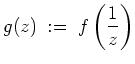Aufgabe.

Es sei 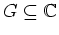$ \mbox{$G\subseteq\mathbb{C}$}$ ein Gebiet derart, daß es ein 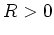$ \mbox{$R>0$}$ gibt mit

$ \mbox{$\displaystyle \{z\in\mathbb{C}\;:\; \vert z\vert>R\} \;\subseteq\; G\;. $}$
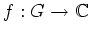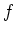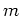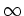Es sei $ \mbox{$f:G\to\mathbb{C}$}$ holomorph. Man sagt, die Funktion $ \mbox{$f$}$ habe eine hebbare Singularität bzw. einen Pol der Ordnung $ \mbox{$m$}$ bzw. eine wesentliche Singularität bei $ \mbox{$\infty$}$ , falls die Funktion
$ \mbox{$\displaystyle g(z) \;:=\; f\left(\frac{1}{z}\right) $}$
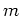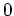eine hebbare Singularität bzw. einen Pol der Ordnung $ \mbox{$m$}$ bzw. eine wesentliche Singularität bei $ \mbox{$0$}$ hat.

Zeige.

  1. Eine ganze Funktion hat eine hebbare Singularität bei 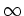$ \mbox{$\infty$}$ genau dann, wenn sie konstant ist.
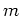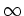  2. Eine ganze Funktion hat einen Pol der Ordnung $ \mbox{$m$}$ bei $ \mbox{$\infty$}$ genau dann, wenn sie ein Polynom vom Grade 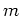$ \mbox{$m$}$ ist.
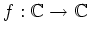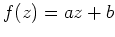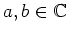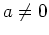  3. Eine ganze bijektive Funktion $ \mbox{$f:\mathbb{C}\to\mathbb{C}$}$ ist von der Form $ \mbox{$f(z)=az+b$}$ mit $ \mbox{$a,b\in\mathbb{C}$}$ und $ \mbox{$a\ne 0$}$ .