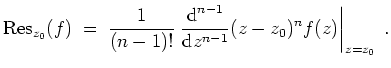Isolierte Singularitäten.
Ist
![]() offen,
offen,
![]() und
und
![]() holomorph,
dann heißt
holomorph,
dann heißt
![]() Singularität (oder auch isolierte Singularität) von
Singularität (oder auch isolierte Singularität) von
![]() .
.
Klassifikation von Singularitäten.
Es seien
![]() eine offene Menge, ein Punkt
eine offene Menge, ein Punkt
![]() und eine holomorphe Funktion
und eine holomorphe Funktion
![]() gegeben.
Die Singularität
gegeben.
Die Singularität
![]() von
von
![]() heißt
heißt
Charakterisierungen.
Es seien
![]() eine offene Menge, ein Punkt
eine offene Menge, ein Punkt
![]() und eine holomorphe Funktion
und eine holomorphe Funktion
![]() gegeben.
gegeben.
(Riemannscher Hebbarkeitssatz) Die Singularität
![]() von
von
![]() ist hebbar genau dann, wenn eine der folgenden äquivalenten
Bedingungen erfüllt ist.
ist hebbar genau dann, wenn eine der folgenden äquivalenten
Bedingungen erfüllt ist.
Die Singularität
![]() von
von
![]() ist ein Pol genau dann, wenn es eine holomorphe Funktion
ist ein Pol genau dann, wenn es eine holomorphe Funktion
![]() und ein
und ein
![]() gibt derart, daß
gibt derart, daß

(Satz von Casorati-Weierstraß) Die Singularität
![]() von
von
![]() ist eine wesentliche Singularität von
ist eine wesentliche Singularität von
![]() genau dann, wenn
genau dann, wenn
![]() in jeder Umgebung von
in jeder Umgebung von
![]() jedem Wert
jedem Wert
![]() beliebig nahe kommt, d.h. zu jedem
beliebig nahe kommt, d.h. zu jedem
![]() gibt
es eine Folge
gibt
es eine Folge
![]() in
in
![]() mit
mit
Laurentreihen.
Für
![]() sei
sei
![]() . Dann heißt
. Dann heißt
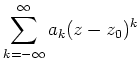
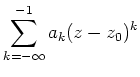
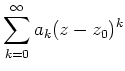
Eine Laurentreihe konvergiert in einem Punkt
![]() genau dann, wenn in diesem Punkt
sowohl der Hauptteil als auch der Nebenteil konvergieren.
genau dann, wenn in diesem Punkt
sowohl der Hauptteil als auch der Nebenteil konvergieren.
Der Konvergenzbereich einer Laurentreihe kann stets durch einen Kreisring beschrieben werden. Genauer, ist
![]() bzw.
bzw.
![]() der Konvergenzradius der Potenzreihe
der Konvergenzradius der Potenzreihe
![]() bzw.
bzw.
![]() , so konvergiert die Laurentreihe
, so konvergiert die Laurentreihe
![]() normal für
normal für
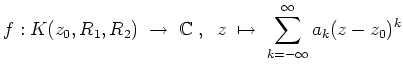
Laurentreihenentwicklung einer holomorphen Funktion.
Es sei
![]() eine holomorphe Funktion. Es seien
eine holomorphe Funktion. Es seien
![]() derart, daß
derart, daß
![]() .
Dann läßt sich
.
Dann läßt sich
![]() als Laurentreihe um
als Laurentreihe um
![]() entwickeln, d.h. es gilt
entwickeln, d.h. es gilt

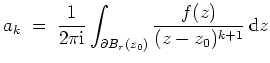
Charakterisierung von Singularitäten mit Hilfe von Laurentreihen.
Es sei
![]() eine Singularität einer holomorphen Funktion
eine Singularität einer holomorphen Funktion
![]() .
Es sei
.
Es sei
![]() derart, daß
derart, daß
![]() . Dann läßt sich die Singularität
. Dann läßt sich die Singularität
![]() von
von
![]() mit Hilfe der Laurentreihenentwicklung
mit Hilfe der Laurentreihenentwicklung
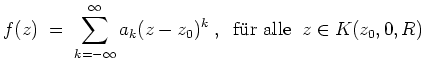
Ist
![]() eine hebbare Singularität, so ist die Laurentreihe von
eine hebbare Singularität, so ist die Laurentreihe von
![]() auf
auf
![]() gleich der Potenzreihenentwicklung
von
gleich der Potenzreihenentwicklung
von
![]() um
um
![]() .
.
Residuen.
Es sei
![]() eine isolierte Singularität einer holomorphen Funktion
eine isolierte Singularität einer holomorphen Funktion
![]() . Es sei
. Es sei
Ist
![]() ein Pol der Ordnung
ein Pol der Ordnung
![]() von
von
![]() , so gilt für das Residuum von
, so gilt für das Residuum von
![]() in
in
![]()