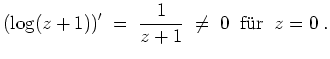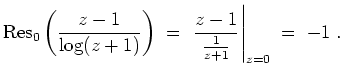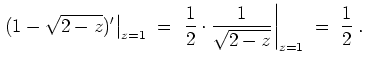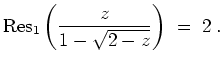- (i)
- Die Funktion
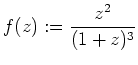 besitzt eine Singularität im Punkt
besitzt eine Singularität im Punkt
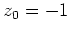 .
Es handelt sich offensichtlich um einen Pol dritter Ordnung.
Das Residuum ist
.
Es handelt sich offensichtlich um einen Pol dritter Ordnung.
Das Residuum ist
- (ii)
- Die Funktion
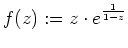 besitzt eine Singularität im Punkt
besitzt eine Singularität im Punkt
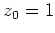 .
Die Laurentreihenentwicklung der Funktion
.
Die Laurentreihenentwicklung der Funktion
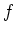 um den Punkt
um den Punkt
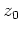 ergibt sich zu
Das Residuum ist also
ergibt sich zu
Das Residuum ist also
- (iii)
- Die Funktion
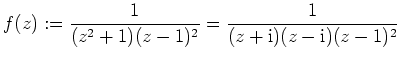 besitzt Singularitäten in den Punkten
besitzt Singularitäten in den Punkten
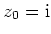 ,
,
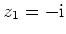 und
und
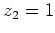 .
Bei
.
Bei
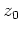 und bei
und bei
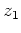 handelt es sich um Pole erster Ordnung, bei
handelt es sich um Pole erster Ordnung, bei
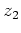 hingegen um einen Pol zweiter Ordnung.
Für die Residuen gilt
hingegen um einen Pol zweiter Ordnung.
Für die Residuen gilt
- (iv)
- Die Funktion
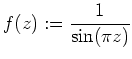 besitzt in allen
besitzt in allen
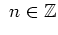 isolierte Singularitäten.
Hierbei handelt es sich um Pole erster Ordnung, da
Die Residuen ergeben sich also zu
isolierte Singularitäten.
Hierbei handelt es sich um Pole erster Ordnung, da
Die Residuen ergeben sich also zu
- (i)
- Der Punkt
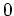 ist
ist
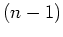 -fache Nullstelle des Zählers und
-fache Nullstelle des Zählers und
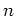 -fache Nullstelle des Nenners.
Also handelt es sich beim Punkt
-fache Nullstelle des Nenners.
Also handelt es sich beim Punkt
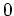 um einen Pol erster Ordnung.
Es gilt
um einen Pol erster Ordnung.
Es gilt
- (ii)
- Beim Punkt
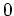 handelt es sich um einen Pol erster Ordnung, da
Es wird
handelt es sich um einen Pol erster Ordnung, da
Es wird
- (iii)
- Es ist
Damit ist das Residuum
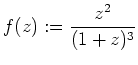 besitzt eine Singularität im Punkt
besitzt eine Singularität im Punkt
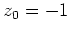 .
Es handelt sich offensichtlich um einen Pol dritter Ordnung.
Das Residuum ist
.
Es handelt sich offensichtlich um einen Pol dritter Ordnung.
Das Residuum ist
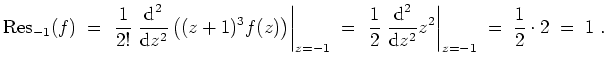
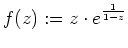 besitzt eine Singularität im Punkt
besitzt eine Singularität im Punkt
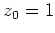 .
Die Laurentreihenentwicklung der Funktion
.
Die Laurentreihenentwicklung der Funktion
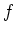 um den Punkt
um den Punkt
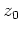 ergibt sich zu
Das Residuum ist also
ergibt sich zu
Das Residuum ist also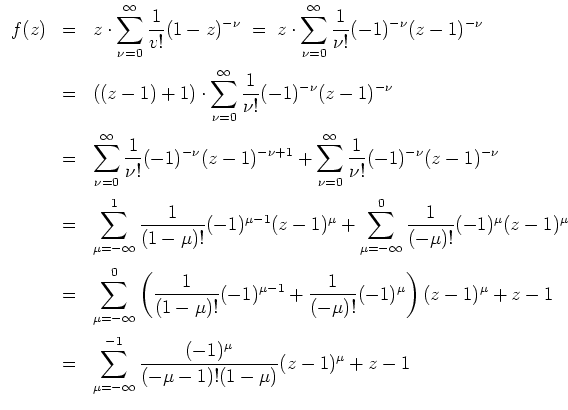
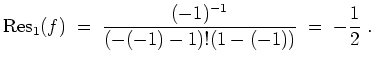
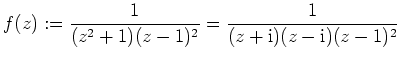 besitzt Singularitäten in den Punkten
besitzt Singularitäten in den Punkten
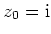 ,
,
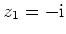 und
und
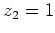 .
Bei
.
Bei
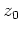 und bei
und bei
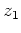 handelt es sich um Pole erster Ordnung, bei
handelt es sich um Pole erster Ordnung, bei
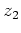 hingegen um einen Pol zweiter Ordnung.
Für die Residuen gilt
hingegen um einen Pol zweiter Ordnung.
Für die Residuen gilt
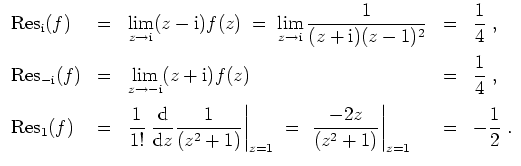
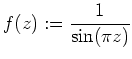 besitzt in allen
besitzt in allen
 isolierte Singularitäten.
Hierbei handelt es sich um Pole erster Ordnung, da
Die Residuen ergeben sich also zu
isolierte Singularitäten.
Hierbei handelt es sich um Pole erster Ordnung, da
Die Residuen ergeben sich also zu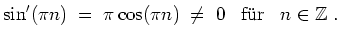
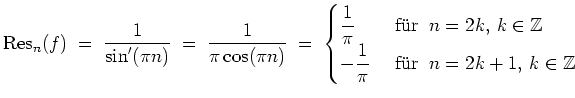
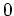 ist
ist
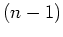 -fache Nullstelle des Zählers und
-fache Nullstelle des Zählers und
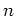 -fache Nullstelle des Nenners.
Also handelt es sich beim Punkt
-fache Nullstelle des Nenners.
Also handelt es sich beim Punkt
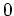 um einen Pol erster Ordnung.
Es gilt
um einen Pol erster Ordnung.
Es gilt
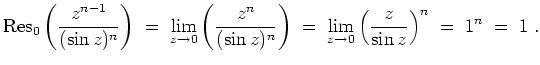
 handelt es sich um einen Pol erster Ordnung, da
Es wird
handelt es sich um einen Pol erster Ordnung, da
Es wird