Alternativlösung: Man betrachte den Spezialfall
![]() in Teil 2.
in Teil 2.
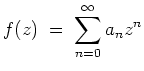
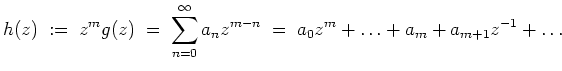
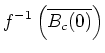
Damit ist
![]() bewiesen. Daraus folgt
bewiesen. Daraus folgt
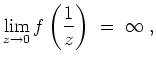
Es sei
![]() , d.h. es gelte
, d.h. es gelte
![]() . Da
. Da
![]() wegen der Injektivität keine weitere Nullstelle haben kann, gilt
wegen der Injektivität keine weitere Nullstelle haben kann, gilt
Alternativlösung: Man betrachte den Spezialfall
![]() in Teil 2.
in Teil 2.
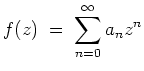
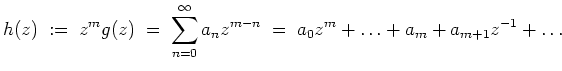
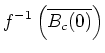
Damit ist
![]() bewiesen. Daraus folgt
bewiesen. Daraus folgt
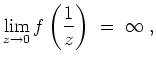
Es sei
![]() , d.h. es gelte
, d.h. es gelte
![]() . Da
. Da
![]() wegen der Injektivität keine weitere Nullstelle haben kann, gilt
wegen der Injektivität keine weitere Nullstelle haben kann, gilt