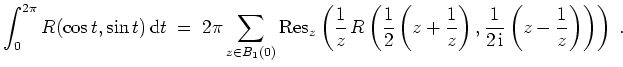Residuensatz.
Es sei
![]() ein Gebiet, und
ein Gebiet, und
![]() sei meromorph auf
sei meromorph auf
![]() . Es sei
. Es sei
![]() ein geschlossener
ein geschlossener
![]() -nullhomologer Weg, auf dem keine Singularitäten von
-nullhomologer Weg, auf dem keine Singularitäten von
![]() liegen. Dann besagt der Residuensatz, daß
liegen. Dann besagt der Residuensatz, daß
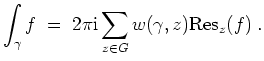
Uneigentliche Integrale der Form
![]() .
.
Es sei
![]() ein Gebiet mit
ein Gebiet mit
![]() , und
, und
![]() seien paarweise verschieden
mit
seien paarweise verschieden
mit
![]() ,
,
![]() .
.
Der erste Satz ermöglicht es, das uneigentliche Integral
![]() einer auf
einer auf
![]() meromorphen
Funktion
meromorphen
Funktion
![]() zu berechnen, sofern sie nur endliche viele Singularitäten hat, und diese nicht auf der reellen Achse liegen.
zu berechnen, sofern sie nur endliche viele Singularitäten hat, und diese nicht auf der reellen Achse liegen.
Es sei
Dann existiert das folgende uneigentliche Riemann-Integral und es gilt
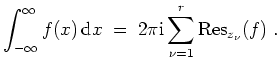
Uneigentliche Integrale der Form
![]() .
.
Dieser Satz ermöglicht es, Integrale vom Typ
![]() zu berechnen,
wobei
zu berechnen,
wobei
![]() im Gegensatz zu obigen Voraussetzungen auch noch endlich viele einfache Pole auf der reellen Achse haben kann.
im Gegensatz zu obigen Voraussetzungen auch noch endlich viele einfache Pole auf der reellen Achse haben kann.
Es seien
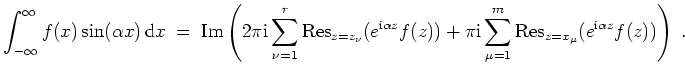
Sind die
![]() nicht Nullstellen von
nicht Nullstellen von
![]() , sondern von
, sondern von
![]() ,
und gelten die obigen Voraussetzungen (i),(iii),(iv) und (v), so gilt
,
und gelten die obigen Voraussetzungen (i),(iii),(iv) und (v), so gilt
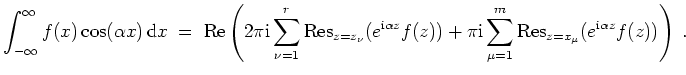
Trigonometrische Integrale.
Es sei
![]() eine rationale Funktion in zwei Veränderlichen, d.h. es gebe Polynome
eine rationale Funktion in zwei Veränderlichen, d.h. es gebe Polynome
![]() mit
mit
![]() .
Ferner gelte
.
Ferner gelte
![]() für alle
für alle
![]() mit
mit
![]() . Dann gilt
. Dann gilt