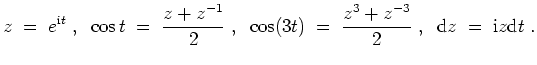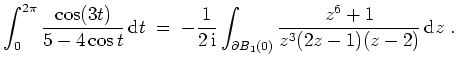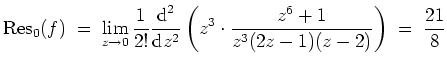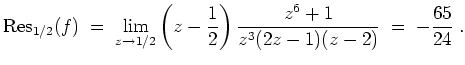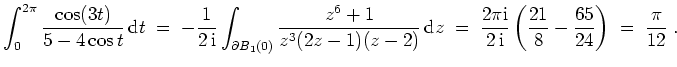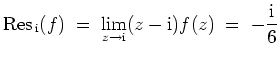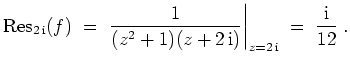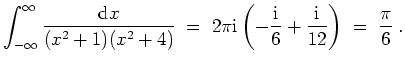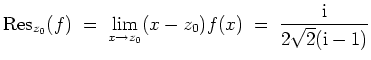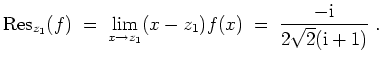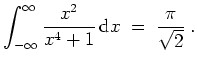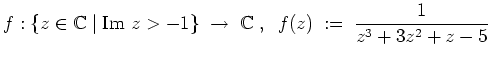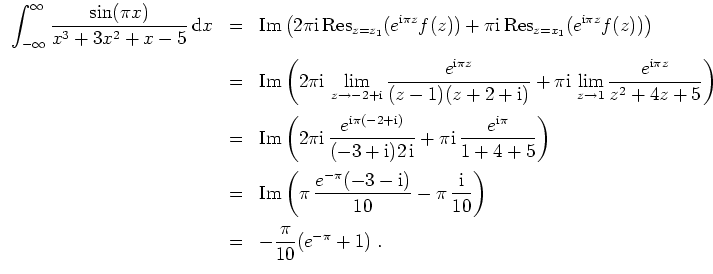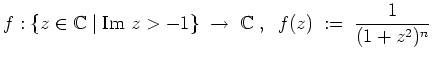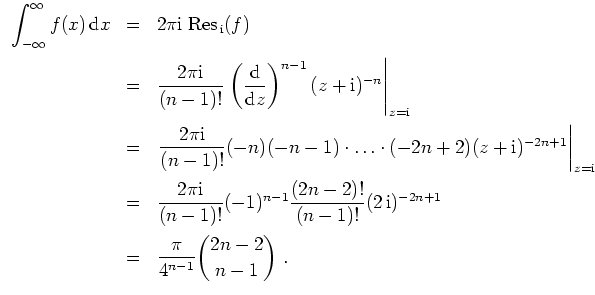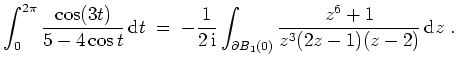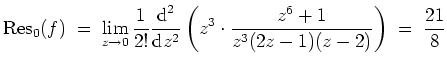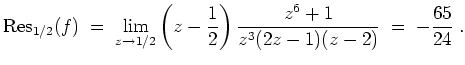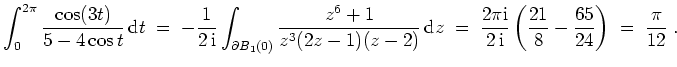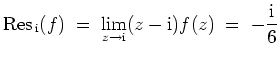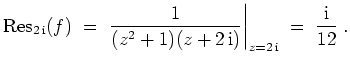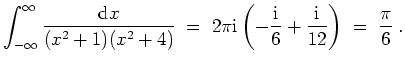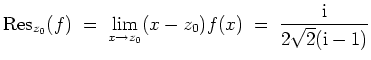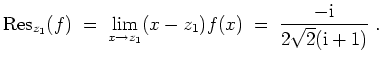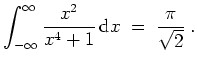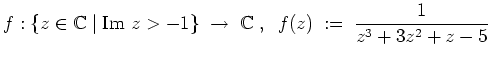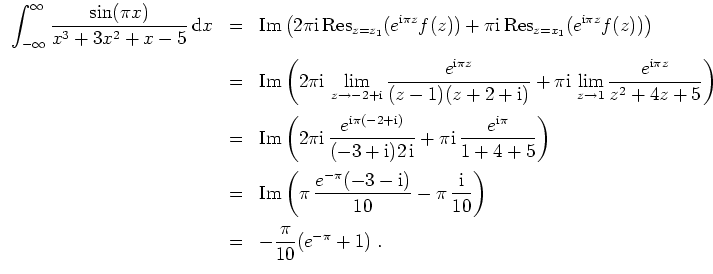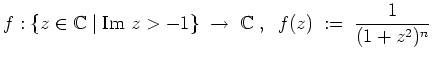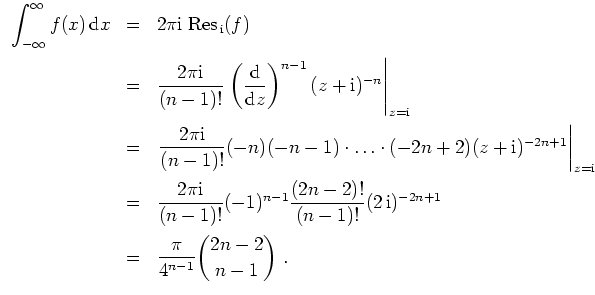- Es gilt
Damit wird
Im Einheitskreis besitzt der Integrand einen Pol der Ordnung drei in
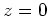 und einen einfachen Pol in
und einen einfachen Pol in
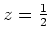 .
Für die Residuen gilt
Nach dem Satz über die Berechnung trigonometrischer Integrale mittels Residuen ergibt sich also
.
Für die Residuen gilt
Nach dem Satz über die Berechnung trigonometrischer Integrale mittels Residuen ergibt sich also
- Die Funktion
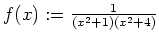 ist bis auf die einfachen Pole
ist bis auf die einfachen Pole
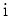 und
und
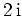 holomorph in der oberen Halbebene.
Die Residuen ergeben sich zu
und
Nach dem Satz über uneigentliche Integrale der Form
holomorph in der oberen Halbebene.
Die Residuen ergeben sich zu
und
Nach dem Satz über uneigentliche Integrale der Form
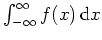 ergibt sich
ergibt sich
- Die Funktion
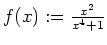 ist holomorph in der oberen Halbebene bis auf die Singularitäten
ist holomorph in der oberen Halbebene bis auf die Singularitäten
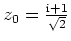 und
und
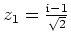 .
Für die Residuen ergibt sich
Die Voraussetzung
ist erfüllt. Nach dem Satz über die Berechnung uneigentlicher Integrale der Form
.
Für die Residuen ergibt sich
Die Voraussetzung
ist erfüllt. Nach dem Satz über die Berechnung uneigentlicher Integrale der Form
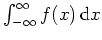 ergibt sich also
ergibt sich also
- Die Funktion
ist holomorph bis auf einfache Pole bei
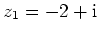 und
und
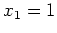 , denn es gilt
Ferner gilt
Nach dem Satz über uneigentliche Integrale der Form
, denn es gilt
Ferner gilt
Nach dem Satz über uneigentliche Integrale der Form
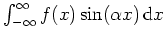 folgt
folgt
- Die Funktion
ist holomorph bis auf einen Pol der Ordnung
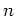 bei
bei
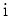 .
Ferner ist
.
Ferner ist
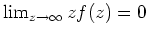 .
Nach dem Satz über die Berechnung von Integralen der Form
.
Nach dem Satz über die Berechnung von Integralen der Form
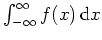 gilt
gilt