Null- und polstellenzählendes Integral und der Satz von Rouche.

Meromorphe Funktionen.

Es sei $ \mbox{$G\subseteq\mathbb{C}$}$ eine offene Menge und $ \mbox{$P\subseteq G$}$ eine diskrete Teilmenge, d.h. $ \mbox{$P$}$ habe keine Häufungspunkte in $ \mbox{$G$}$ . Unter einer meromorphen Funktion auf $ \mbox{$G$}$ verstehen wir eine Funktion $ \mbox{$f:G\to\mathbb{C}_\infty$}$ derart, daß

Eine meromorphe Funktion auf $ \mbox{$G$}$ ist stetig als Funktion $ \mbox{$G\to\mathbb{C}_\infty$}$ .

Ist $ \mbox{$f$}$ meromorph auf $ \mbox{$G$}$ und $ \mbox{$z_0\in G$}$ , so definieren wir die Ordnung von $ \mbox{$z_0$}$ bezüglich $ \mbox{$f$}$ durch

$ \mbox{$\displaystyle \text{ord}(f,z_0) \;:=\; \begin{cases}m, & \text{falls {... ...n Pol der Ordnung {$\mbox{$m\ge 1$}$} ist}\\ 0, &\text{sonst.} \end{cases}$}$
Die Ordnung $ \mbox{$m=\text{ord}(f,z_0)$}$ ist dadurch eindeutig bestimmt, daß die Funktion $ \mbox{$g(z):=\frac{f(z)}{(z-z_0)^m}$}$ in $ \mbox{$z_0$}$ eine hebbare Singularität mit $ \mbox{$g(z_0)\ne 0$}$ besitzt. Es gilt dann
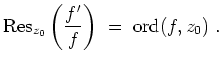
$ \mbox{$\displaystyle \text{Res}_{z_0}\left(\frac{f'}{f}\right) \;=\; \text{ord}(f,z_0)\;. $}$

Null- und polstellenzählendes Integral.

Es seien $ \mbox{$G\subseteq\mathbb{C}$}$ ein Gebiet, $ \mbox{$f$}$ eine auf $ \mbox{$G$}$ meromorphe Funktion und $ \mbox{$g$}$ eine auf $ \mbox{$G$}$ holomorphe Funktion. Ferner sei $ \mbox{$\gamma$}$ ein geschlossener $ \mbox{$G$}$ -nullhomologer Weg, auf dem weder Null- noch Polstellen von $ \mbox{$f$}$ liegen. Dann gilt

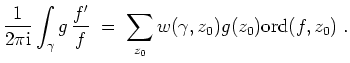
$ \mbox{$\displaystyle \frac{1}{2\pi\text{i}} \int_\gamma g\,\frac{f'}{f} \;=\; \sum_{z_0} w(\gamma,z_0)g(z_0)\text{ord}(f,z_0)\;. $}$
Dabei wird über die endlich vielen Null- und Polstellen von $ \mbox{$f$}$ im Inneren von $ \mbox{$\gamma$}$ summiert.

Ist speziell $ \mbox{$\gamma=\partial B_r(w)$}$ und $ \mbox{$g(z):=1$}$ , so zählt $ \mbox{$\int_\gamma\frac{f'}{f}$}$ die Anzahl der Nullstellen von $ \mbox{$f$}$ minus die Anzahl der Polstellen von $ \mbox{$f$}$ in $ \mbox{$B_r(w)$}$ , jeweils mit Vielfachheiten gezählt.

Satz von Rouché.

Es sei $ \mbox{$G\subseteq\mathbb{C}$}$ ein Gebiet, und $ \mbox{$f$}$ und $ \mbox{$g$}$ seien auf $ \mbox{$G$}$ meromorphe Funktionen. Ferner sei $ \mbox{$\gamma$}$ ein geschlossener $ \mbox{$G$}$ -nullhomologer Weg, auf dem weder Null- noch Polstellen von $ \mbox{$f$}$ , noch von $ \mbox{$g$}$ liegen. Es gelte

$ \mbox{$\displaystyle \vert f(z)+g(z)\vert \;<\; \vert f(z)\vert+\vert g(z)\vert\;,\;\;\text{f\uml ur alle}\;\;z\in\mathcal{T}(\gamma)\;. $}$
Dann ist
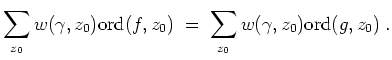
$ \mbox{$\displaystyle \sum_{z_0} w(\gamma,z_0)\text{ord}(f,z_0) \;=\; \sum_{z_0} w(\gamma,z_0)\text{ord}(g,z_0)\;. $}$
Dabei wird jeweils über die endlich vielen Null- und Polstellen von $ \mbox{$f$}$ bzw. $ \mbox{$g$}$ im Inneren von $ \mbox{$\gamma$}$ summiert.

Ist speziell $ \mbox{$\gamma=\partial B_r(w)$}$ , sind $ \mbox{$f$}$ und $ \mbox{$g$}$ holomorph auf $ \mbox{$B_{r+\varepsilon}(w)$}$ für ein $ \mbox{$\varepsilon>0$}$ , und gilt $ \mbox{$\vert f+g\vert<\vert f\vert+\vert g\vert$}$ auf $ \mbox{$\partial B_r(w)$}$ , so haben $ \mbox{$f$}$ und $ \mbox{$g$}$ gleich viele Nullstellen in $ \mbox{$B_r(w)$}$ , jeweils mit Vielfachheiten gezählt.