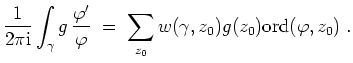Für jede holomorphe Funktion
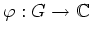 gilt nach der Formel für das null- und
polstellenzählende Integral
gilt nach der Formel für das null- und
polstellenzählende Integral
Es sei nun
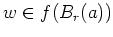 gegeben und
gegeben und
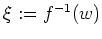 .
Wir wenden obige Formel an auf
.
Wir wenden obige Formel an auf
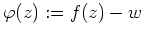 und
und
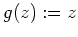 .
Wegen der Injektivität von
.
Wegen der Injektivität von
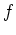 ist
ist
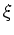 die einzige Nullstelle von
die einzige Nullstelle von
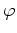 auf
auf
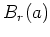 , und diese ist einfach.
Also ergibt sich
, und diese ist einfach.
Also ergibt sich
![]() gilt nach der Formel für das null- und
polstellenzählende Integral
gilt nach der Formel für das null- und
polstellenzählende Integral