Lösung.

  1. Die Menge $ \mbox{$K:=\partial B_r(z_0)$}$ ist kompakt. Daher gilt
    $ \mbox{$\displaystyle m \;:=\; \min\{\vert f(z)\vert\;:\; z\in K\} \;>0\;. $}$
    Wegen der kompakten Konvergenz gibt es ein $ \mbox{$N\ge m$}$ derart, daß für alle $ \mbox{$n\ge N$}$ und $ \mbox{$z\in K$}$ gilt, daß
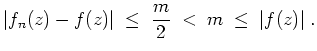
    $ \mbox{$\displaystyle \vert f_n(z)-f(z)\vert \;\le\; \dfrac{m}{2} \;<\; m \;\le\; \vert f(z)\vert\;. $}$
    Nach dem Satz für Rouché haben daher $ \mbox{$f_n$}$ und $ \mbox{$f$}$ auf $ \mbox{$B_r(z_0)$}$ gleich viele Nullstellen.

  2. Es sei $ \mbox{$f$}$ nicht identisch $ \mbox{$0$}$ auf $ \mbox{$G$}$ . Wir nehmen an, es gäbe ein $ \mbox{$z_0\in G$}$ mit $ \mbox{$f(z_0)=0$}$ . Wegen der Isoliertheit der Nullstellen gibt es ein $ \mbox{$r>0$}$ derart, daß
    $ \mbox{$\displaystyle f(z)\;\ne\;0\;,\;\;\text{f\uml ur alle}\;\; z\in\overline{B_r(z_0)}\setminus\{z_0\}\;. $}$
    Nach 1. gibt es ein $ \mbox{$N\ge m$}$ derart, daß für alle $ \mbox{$n\ge N$}$ die Funktionen $ \mbox{$f_n$}$ und $ \mbox{$f$}$ gleich viele Nullstellen auf $ \mbox{$B_r(z_0)$}$ haben. Nach Voraussetzung hat aber $ \mbox{$f_n$}$ dort keine Nullstelle, während nach unserer Annahme $ \mbox{$f$}$ dort eine Nullstelle hat; das ist ein Widerspruch.

  3. Es sei $ \mbox{$f$}$ nicht konstant auf $ \mbox{$G$}$ . Wir nehmen an, es gäbe $ \mbox{$z_1,z_2\in G$}$ mit $ \mbox{$z_1\ne z_2$}$ und $ \mbox{$w:=f(z_1)=f(z_2)$}$ . Dann sind $ \mbox{$z_1$}$ und $ \mbox{$z_2$}$ Nullstellen der Funktion $ \mbox{$f-w$}$ , und wegen der Isoliertheit der Nullstellen gibt es ein $ \mbox{$r>0$}$ derart, daß $ \mbox{$f-w$}$ auf $ \mbox{$\overline{B_r(z_1)}$}$ und $ \mbox{$\overline{B_r(z_2)}$}$ keine weiteren Nullstellen hat. Wir wählen $ \mbox{$r$}$ so klein, daß $ \mbox{$B_r(z_1)$}$ und $ \mbox{$B_r(z_2)$}$ zusätzlich noch disjunkt sind.

    Aus den Voraussetzungen folgt auch, daß die Funktionenfolge $ \mbox{$(f_n-w)_{n\ge m}$}$ kompakt auf $ \mbox{$G$}$ gegen $ \mbox{$f-w$}$ konvergiert.

    Nach 1. gibt es daher ein $ \mbox{$N\ge m$}$ so, daß für alle $ \mbox{$n\ge N$}$ die Funktionen $ \mbox{$f_n-w$}$ und $ \mbox{$f-w$}$ gleich viele Nullstellen auf $ \mbox{$B_r(z_1)$}$ bzw. $ \mbox{$B_r(z_2)$}$ besitzen. Für alle $ \mbox{$n\ge N$}$ hat daher $ \mbox{$f_n-w$}$ sowohl auf $ \mbox{$B_r(z_1)$}$ als auch auf $ \mbox{$B_r(z_2)$}$ mindestens eine Nullstelle, im Widerspruch zur Injektivität von $ \mbox{$f_n$}$ .