Aufgabe.

Es sei 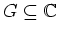ein Gebiet und 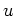sei harmonisch auf 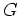. Zeige.

1. Ist 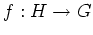holomorph, so ist 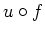harmonisch auf .
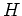2. Es sei 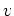harmonisch auf 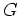, und 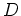sei eine offene Kreisscheibe in 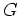mit 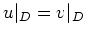. Dann gilt 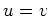. (Identitätssatz für harmonische Funktionen)
3. Zeige, daß im obigen Identitätssatz 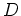nicht durch eine beliebige Teilmenge mit einem Häufungspunkt in 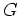ersetzt werden kann.
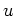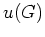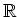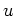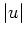4. Ist nicht konstant, so ist ein offenes Intervall in . Insbesondere nimmt weder noch auf 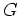ein Maximum an. (Gebietstreue und Maximumprinzip für harmonische Funktionen)
5. Es sei 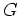beschränkt und 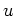sei zusätzlich stetig auf 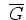. Dann ist 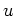durch seine Werte auf 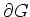eindeutig bestimmt.