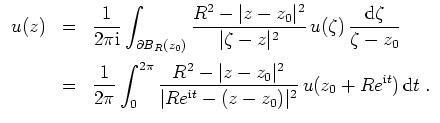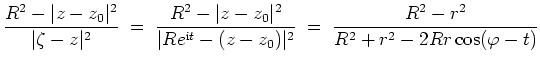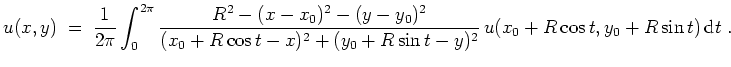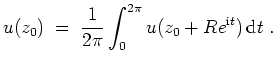Definition.
Es sei
![]() eine offene Menge. Eine Funktion
eine offene Menge. Eine Funktion
![]() heißt harmonisch, falls sie zweimal stetig
partiell differenzierbar ist, und die Laplacesche Differentialgleichung
heißt harmonisch, falls sie zweimal stetig
partiell differenzierbar ist, und die Laplacesche Differentialgleichung
Eigenschaften.
Es sei
![]() eine offene Menge, und
eine offene Menge, und
![]() sei eine Funktion. Dann sind folgende Eigenschaften äquivalent.
sei eine Funktion. Dann sind folgende Eigenschaften äquivalent.
Poissonsche Integralformel.
Es sei
![]() harmonisch auf einem Gebiet
harmonisch auf einem Gebiet
![]() . Es sei
. Es sei
![]() derart, daß
derart, daß
![]() . Es sei
. Es sei
![]() .
Dann besagt die Poissonsche Integralformel, daß
.
Dann besagt die Poissonsche Integralformel, daß