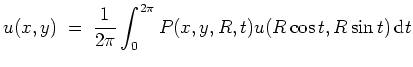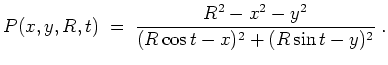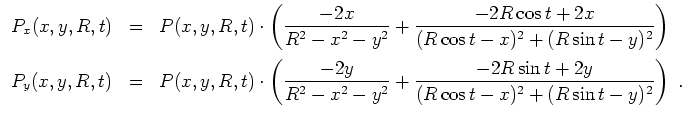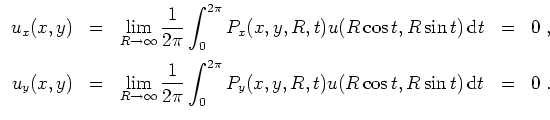Wir wenden die reelle Schreibweise der Poissonschen Integralformel mit
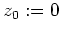 und
und
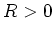 beliebig an und erhalten
beliebig an und erhalten
mit dem Poisson-Kern
Es gilt
Insbesondere folgt wegen
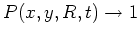 für
für
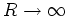 , daß
Daraus folgt wegen der Beschränktheit von
, daß
Daraus folgt wegen der Beschränktheit von
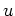 Daher ist
Daher ist
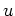 konstant auf
konstant auf
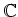 .
.
![]() und
und
![]() beliebig an und erhalten
beliebig an und erhalten