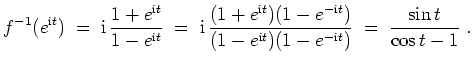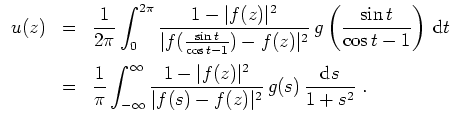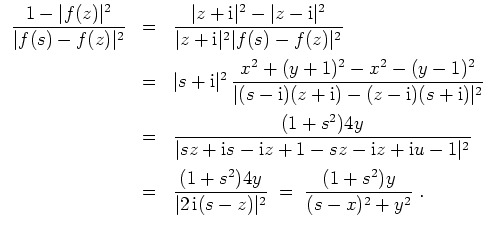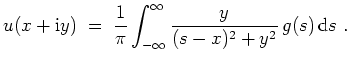Aus der Theorie der Möbiustransformationen ist bekannt, daß die Abbildung
stetig und bijektiv ist und die obere Halbebene
 konform auf das Innere
konform auf das Innere
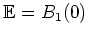 des
Einheitskreises abbildet. Außerdem ist die Funktion
des
Einheitskreises abbildet. Außerdem ist die Funktion
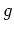 stetig auf
stetig auf
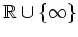 .
Daher ist die Funktion
ebenfalls stetig.
Also gibt es genau eine stetige Funktion
.
Daher ist die Funktion
ebenfalls stetig.
Also gibt es genau eine stetige Funktion
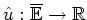 mit
mit
Folglich ist
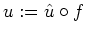 stetig und erfüllt die geforderten Eigenschaften. Die Eindeutigkeit von
stetig und erfüllt die geforderten Eigenschaften. Die Eindeutigkeit von
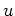 folgt aus der Eindeutigkeit von
folgt aus der Eindeutigkeit von
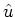 und der Umkehrbarkeit von
und der Umkehrbarkeit von
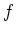 .
.
Gemäß der Poissonschen Integralformel gilt
für alle
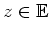 . Also gilt für alle
. Also gilt für alle
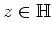 Es gilt
Es gilt
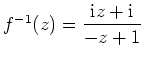 und daher
Es folgt mit der Substitution
und daher
Es folgt mit der Substitution
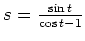 Schreibt man
Schreibt man
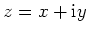 , so ergibt sich
Setzt man dies in obige Gleichung ein, so erhält man
, so ergibt sich
Setzt man dies in obige Gleichung ein, so erhält man
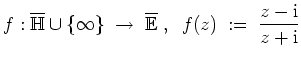
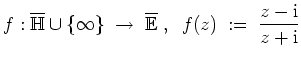
![]() stetig und erfüllt die geforderten Eigenschaften. Die Eindeutigkeit von
stetig und erfüllt die geforderten Eigenschaften. Die Eindeutigkeit von
![]() folgt aus der Eindeutigkeit von
folgt aus der Eindeutigkeit von
![]() und der Umkehrbarkeit von
und der Umkehrbarkeit von
![]() .
.
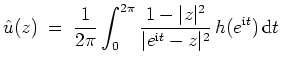
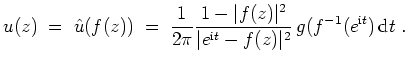
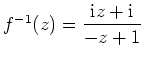 und daher
und daher