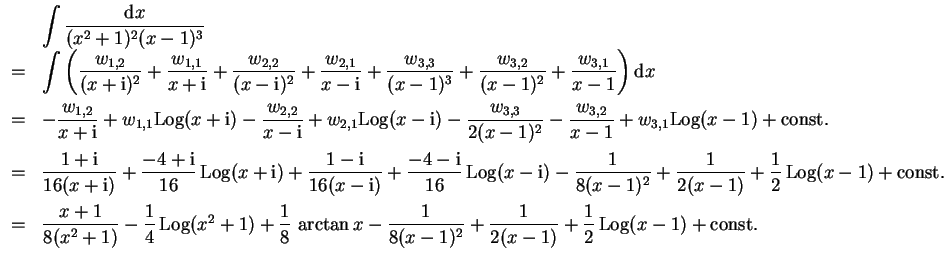Wir setzen an mit
wozu wir die Nullstellen des Nenners mit
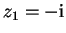 ,
,
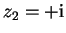 und
und
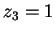 bezeichnen.
bezeichnen.
Mit Zuhaltemethode wird zunächst
Subtraktion der bekannten Terme reduziert das Problem auf die Behandlung von
Mit Zuhaltemethode wird nun
Subtraktion der bekannten Terme reduziert das Problem auf die Behandlung von
woraus schließlich
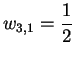 folgt.
folgt.
Damit können wir das Integral berechnen.
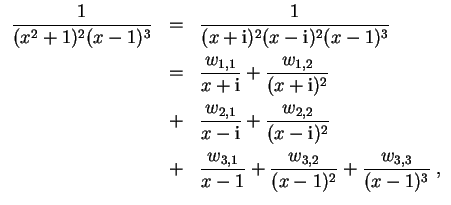
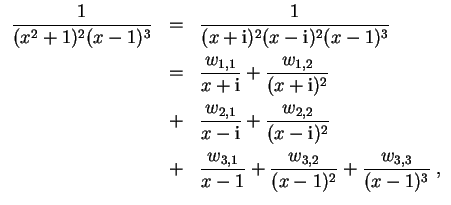
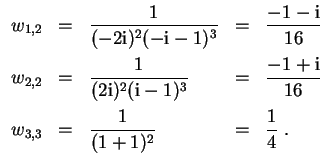
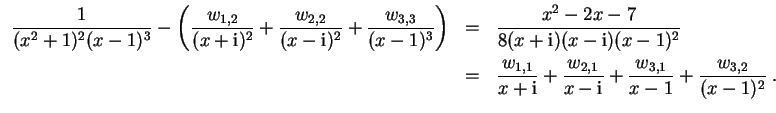
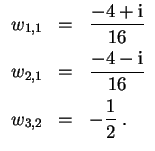
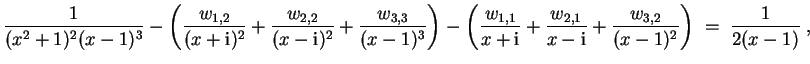
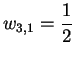 folgt.
folgt.