Wir erhalten dann mit der Substitution
![]() und
und
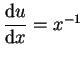
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle\int _3^\infty\frac{{\mb...
...m_{t\to\infty} [(1-\alpha)^{-1} u^{1-\alpha}]_{\log 3}^t\; , \\
\end{array}$}$](img5.gif)
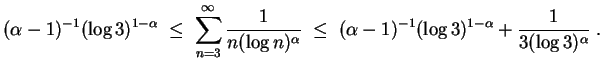
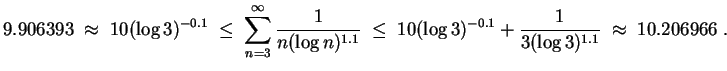
Wir erhalten dann mit der Substitution
![]() und
und
![$ \mbox{${\displaystyle\frac{{\mbox{d}}u}{{\mbox{d}}x}} = \prod_{\nu = 0}^{m-1} (\log^{[\nu]} x)^{-1}$}$](img15.gif)
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle\int _N^\infty\frac{{\mb...
...o\infty} [(1-\alpha)^{-1} u^{1-\alpha}]_{\log^{[m]} N}^t\; , \\
\end{array}$}$](img16.gif)
![$ \mbox{$\displaystyle
(\alpha-1)^{-1}(\log^{[m]} N)^{1-\alpha}
\;\leq\;\sum_{n...
...frac{1}{(\log^{[m]} N)^\alpha\cdot \prod_{\nu = 0}^{m-1} \log^{[\nu]} N}\; .
$}$](img18.gif)
Wir erhalten dann mit der Substitution
![]() und
und
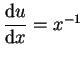
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle\int _3^\infty\frac{{\mb...
...m_{t\to\infty} [(1-\alpha)^{-1} u^{1-\alpha}]_{\log 3}^t\; , \\
\end{array}$}$](img5.gif)
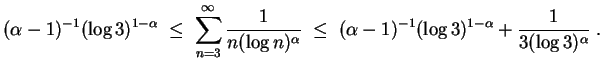
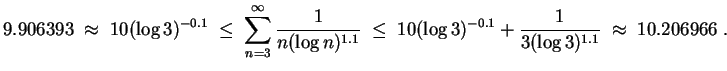
Wir erhalten dann mit der Substitution
![]() und
und
![$ \mbox{${\displaystyle\frac{{\mbox{d}}u}{{\mbox{d}}x}} = \prod_{\nu = 0}^{m-1} (\log^{[\nu]} x)^{-1}$}$](img15.gif)
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle\int _N^\infty\frac{{\mb...
...o\infty} [(1-\alpha)^{-1} u^{1-\alpha}]_{\log^{[m]} N}^t\; , \\
\end{array}$}$](img16.gif)
![$ \mbox{$\displaystyle
(\alpha-1)^{-1}(\log^{[m]} N)^{1-\alpha}
\;\leq\;\sum_{n...
...frac{1}{(\log^{[m]} N)^\alpha\cdot \prod_{\nu = 0}^{m-1} \log^{[\nu]} N}\; .
$}$](img18.gif)
Skizze von
![]() .
.
![\includegraphics[width = 10cm]{s1_log3.eps}](img20.gif)