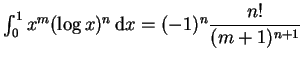 . Induktion nach
. Induktion nach
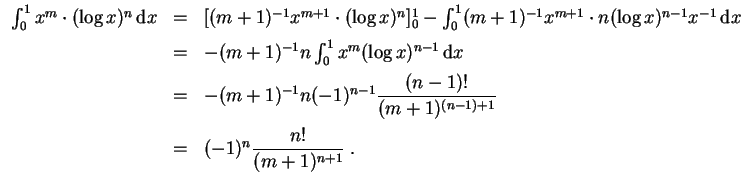
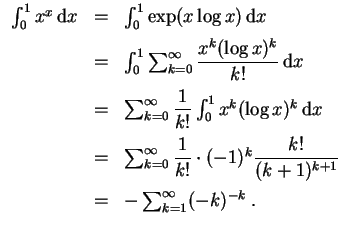
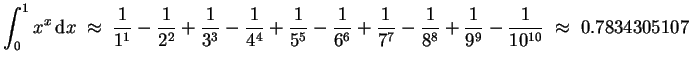
(In diesem Sinne stellt die angegebene Reihe in der Tat eine praktikable Berechnung des fraglichen Integrals dar.)
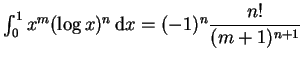 . Induktion nach
. Induktion nach
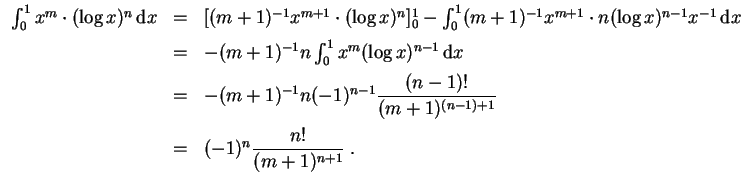
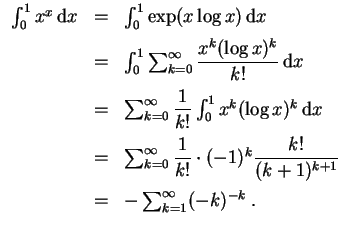
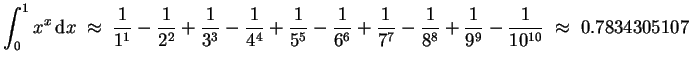
(In diesem Sinne stellt die angegebene Reihe in der Tat eine praktikable Berechnung des fraglichen Integrals dar.)
Skizze zu
![]() .
.
![\includegraphics[width = 8cm]{s2_x^x.eps}](img11.gif)