Lösung.

Die zugehörige homogene Gleichung hat die Lösung

$ \mbox{$\displaystyle I(t) \;=\; C\,e^{-tR/L} \;. $}$
Die partikuläre Lösung erhalten wir durch Variation der Konstanten aus
$ \mbox{$\displaystyle L\dot{C}(t) e^{-tR/L} \;=\; U(t) \;=\; U_0\cos(\omega t)\;, $}$
also
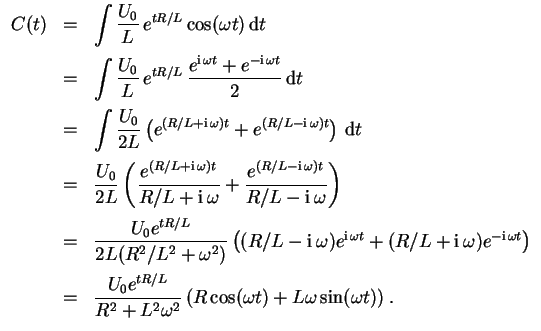
$ \mbox{$\displaystyle \begin{array}{rcl} C(t) &=& \displaystyle\int {\displays... ...L}}{R^2+L^2\omega^2}}\,(R\cos(\omega t)+L\omega\sin(\omega t))\;. \end{array}$}$

Dies kann wie folgt als Phasenverschiebung im Vergleich zur anliegenden Spannung gedeutet werden. Sei

$ \mbox{$\displaystyle \delta \;:=\; \arctan(\omega L/R) \;. $}$
Dann ist wegen
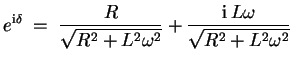
$ \mbox{$\displaystyle e^{\mathrm{i}\delta} \;=\; {\displaystyle\frac{R}{\sqrt{... ...omega^2}}}+{\displaystyle\frac{\mathrm{i}\,L\omega}{\sqrt{R^2+L^2\omega^2}}} $}$
also
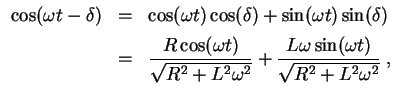
$ \mbox{$\displaystyle \begin{array}{rcl} \cos(\omega t-\delta) &=& \cos(\omega... ...playstyle\frac{L\omega\sin(\omega t)}{\sqrt{R^2+L^2\omega^2}}}\;, \end{array}$}$
und daher
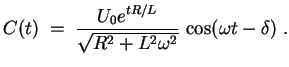
$ \mbox{$\displaystyle C(t) \;=\; {\displaystyle\frac{U_0e^{tR/L}}{\sqrt{R^2+L^2\omega^2}}}\,\cos(\omega t-\delta)\;. $}$
Die allgemeine Lösung ist also
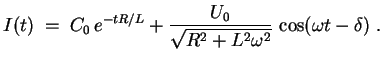
$ \mbox{$\displaystyle I(t) \;=\; C_0\,e^{-tR/L} + {\displaystyle\frac{U_0}{\sqrt{R^2+L^2\omega^2}}}\,\cos(\omega t-\delta)\;. $}$
Die Bedingung $ \mbox{$I(0)=0$}$ liefert
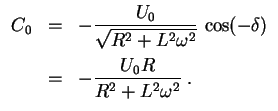
$ \mbox{$\displaystyle \begin{array}{rcl} C_0 &=& - {\displaystyle\frac{U_0}{\... ...*{2mm}\\ &=& - {\displaystyle\frac{U_0 R}{R^2+L^2\omega^2}} \;. \end{array}$}$

Für $ \mbox{$R=1$}$, $ \mbox{$L=1$}$, $ \mbox{$U_0=1$}$ und $ \mbox{$\omega=1$}$ erhalten wir diese Lösung auch aus dem folgenden Richtungsfeld.

\includegraphics[width=15cm]{p2_dfield.eps}