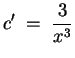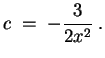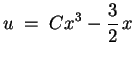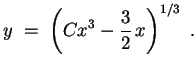Dies ist eine Bernoullische Gleichung mit Exponent
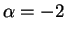 .
.
Die Substitution
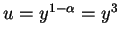 führt zur linearen Gleichung
führt zur linearen Gleichung
Die homogene Gleichung
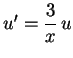 hat die allgemeine Lösung
hat die allgemeine Lösung
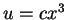 .
Die inhomogene Gleichung wird durch Variation der Konstanten gelöst. Der Ansatz
.
Die inhomogene Gleichung wird durch Variation der Konstanten gelöst. Der Ansatz
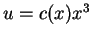 führt zu
und somit zu
Die allgemeine Lösung für
führt zu
und somit zu
Die allgemeine Lösung für
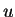 ist also
mit einer Konstanten
ist also
mit einer Konstanten
 , und für
, und für
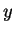 ergibt sich
ergibt sich
![]() .
.
![]() führt zur linearen Gleichung
führt zur linearen Gleichung
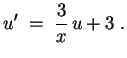
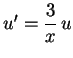 hat die allgemeine Lösung
hat die allgemeine Lösung