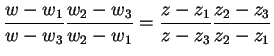Seien
![]() mit
mit
![]() . Sei die zugehörige Möbiustransformation definiert als
. Sei die zugehörige Möbiustransformation definiert als
![]() , wobei
, wobei
![]() Werte in
Werte in
![]() annehmen darf und
annehmen darf und
![]() auch Werte in diesem Bereich liefert.
auch Werte in diesem Bereich liefert.
Ein verallgemeinerter Kreis ist per Definition entweder ein Kreis oder eine Gerade. Eine Möbiustransformation bildet einen verallgemeinerten Kreis auf einen verallgemeinerten Kreis ab.
Seien nun
![]() ,
,
![]() und
und
![]() drei verschiedene Punkte aus
drei verschiedene Punkte aus
![]() , und seien
, und seien
![]() ,
,
![]() und
und
![]() ebenfalls drei verschiedene Punkte aus
ebenfalls drei verschiedene Punkte aus
![]() . Es gibt genau
eine Möbiustransformation, die
. Es gibt genau
eine Möbiustransformation, die
![]() auf
auf
![]() ,
,
![]() auf
auf
![]() und
und
![]() auf
auf
![]() abbildet. Diese erhält man, indem man die 6-Punkte-Formel
abbildet. Diese erhält man, indem man die 6-Punkte-Formel