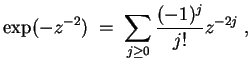Auf
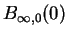 ist
ist
mithin liegt eine wesentliche Singularität vor.
Sei
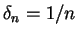 , sei
, sei
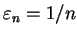 , sei
, sei
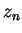 nach Casorati-Weierstraß so
gewählt, daß
nach Casorati-Weierstraß so
gewählt, daß
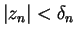 und
und
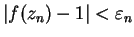 .
Dann gelten
.
Dann gelten
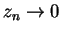 und
und
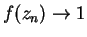 für
für
 .
.
Schließlich ist
d.h. je nach dem, wie die Singularität approximiert wird,
kann man unterschiedliche Grenzwerte erhalten.
![]() ist
ist