(i) Nach Definition gilt
![]() .
Für
.
Für
![]() gelten für
gelten für
![]() die folgenden Identitäten
die folgenden Identitäten
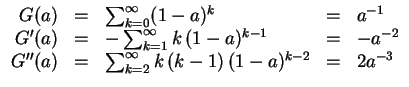
Für den Erwartungswert folgt
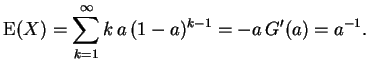
Für
![]() gilt
gilt
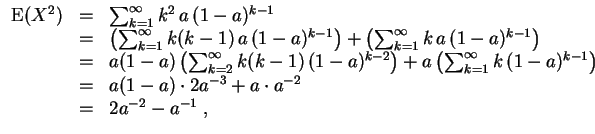
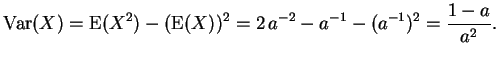
(ii) Beim Würfeln ist obige Überlegung anwendbar mit
![]() , d.h. die Anzahl die
mittleren erwarteten Wiederholungen bis zur ersten geworfenen Eins ist
, d.h. die Anzahl die
mittleren erwarteten Wiederholungen bis zur ersten geworfenen Eins ist
![]() .
.