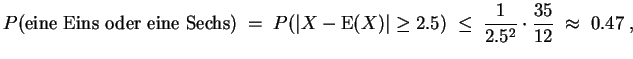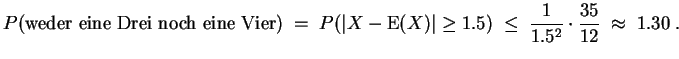Für die Approximation mit der Ungleichung von Chebyshev
beschreibe die Zufallsvariable
![]() die
Augenanzahl, d.h.
die
Augenanzahl, d.h.
![]() für
für
![]() .
.
Dann gilt
![]() und
und
![]() .
.
Die exakte Wahrscheinlichkeit für das jeweilige Ereignis kann direkt im Laplaceschen Wahrscheinlichkeitsraum abgelesen werden.