Die Folge der Zufallsvariablen
![]() , die den Münzwurf beschreibt
(
, die den Münzwurf beschreibt
(
![]() ,
,
![]() )
ist unabhängig, und es gilt
)
ist unabhängig, und es gilt
![]() und
und
![]() für alle
für alle
![]() .
.
Wir hatten mit
![]() den Mittelwert der ersten
den Mittelwert der ersten
![]() Würfe bezeichnet. Es ist
Würfe bezeichnet. Es ist
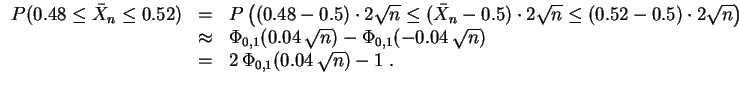
Gefragt ist
![]() mit
mit
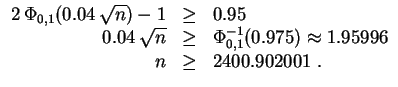
Die Münze muß somit mindestens
![]() -mal geworfen werden.
-mal geworfen werden.