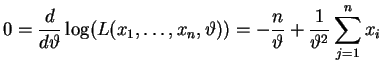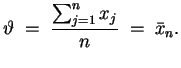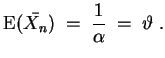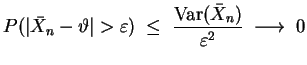Die Likelihood-Funktion ist
falls alle
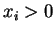 und ansonsten gleich null.
und ansonsten gleich null.
Die Likelihood-Funktion
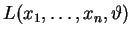 für
für
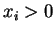 ist genau
da maximal, wo auch
ist genau
da maximal, wo auch
 maximal ist, d.h. die notwendige
Bedingung ist
maximal ist, d.h. die notwendige
Bedingung ist
und damit ist
Der zugehörige Maximum-Likelihood-Schätzer ist also
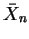 .
.
Es gilt
Da
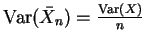 , gilt mit der Ungleichung von Chebyshev für
gegebenes
, gilt mit der Ungleichung von Chebyshev für
gegebenes
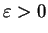 für
für
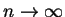 .
Somit ist die Folge der Schätzfunktionen
.
Somit ist die Folge der Schätzfunktionen
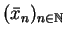 konsistent.
konsistent.
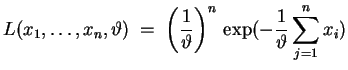
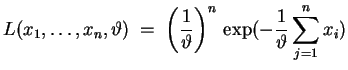
![]() für
für
![]() ist genau
da maximal, wo auch
ist genau
da maximal, wo auch
![]() maximal ist, d.h. die notwendige
Bedingung ist
maximal ist, d.h. die notwendige
Bedingung ist