Es ist
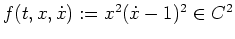 und
und
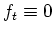 . Nehmen wir an, es sei
. Nehmen wir an, es sei
![$ \mbox{$x \in C^2[-1,1]$}$](img14.png) eine Extremale
von
eine Extremale
von
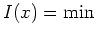 , so ist
konstant. Wegen
, so ist
konstant. Wegen
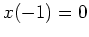 ist
ist
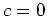 . Es folgt also
. Es folgt also
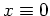 oder
oder
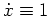 , d.h.
, d.h.
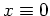 oder
oder
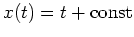 . Diese Funktionen erfüllen jedoch nicht die Randbedingungen
unseres Variationsproblems, so dass es keine
. Diese Funktionen erfüllen jedoch nicht die Randbedingungen
unseres Variationsproblems, so dass es keine
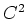 -Funktion geben kann, die dieses Problem minimiert.
-Funktion geben kann, die dieses Problem minimiert.
Offensichtlich ist aber die Funktion
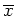 mit
mit
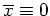 auf
auf
![$ \mbox{$[-1,0]$}$](img24.png) und
und
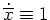 auf
auf
![$ \mbox{$(0,1]$}$](img26.png) , d.h.
, d.h.
ein globales Minimum von
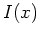 . Es ist nämlich
. Es ist nämlich
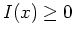 für alle
für alle
![$ \mbox{$x \in C_s^1[-1,1]$}$](img30.png) und
und
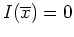 .
.
![$ \mbox{$\displaystyle
\int_0^1 \dot x \; \text{d}t = [x]_0^1 = x(1) - x(0) = 1
$}$](img1.png)
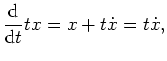
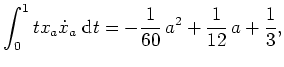
![]() mit
mit
![]() auf
auf
![]() und
und
![]() auf
auf
![]() , d.h.
, d.h.
![$ \mbox{$\displaystyle
\overline x(t) = \begin{cases}
0, & t \in [-1,0]\\
t, & t \in (0,1],
\end{cases} $}$](img27.png)
![$ \mbox{$\displaystyle
\int_0^1 \dot x \; \text{d}t = [x]_0^1 = x(1) - x(0) = 1
$}$](img1.png)
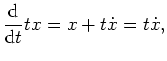
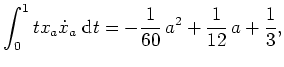
![]() mit
mit
![]() auf
auf
![]() und
und
![]() auf
auf
![]() , d.h.
, d.h.
![$ \mbox{$\displaystyle
\overline x(t) = \begin{cases}
0, & t \in [-1,0]\\
t, & t \in (0,1],
\end{cases} $}$](img27.png)