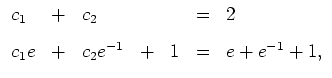Gemäß der Eulerschen Differentialgleichung gilt
auf
![$ \mbox{$[0,1]$}$](img2.png) .
.
Die allgemeine Lösung dieser linearen Differentialgleichung zweiter Ordnung ist gegeben durch
mit Konstanten
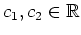 . Die Randbedingungen des vorliegenden Variationsproblems führen auf die
Gleichungen
also folgt
. Die Randbedingungen des vorliegenden Variationsproblems führen auf die
Gleichungen
also folgt
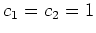 . Es gibt somit genau eine Lösung der Eulerschen Differentialgleichung, die die Randbedingungen
erfüllt. Diese ist gegeben durch
. Es gibt somit genau eine Lösung der Eulerschen Differentialgleichung, die die Randbedingungen
erfüllt. Diese ist gegeben durch