- Aus der Eulerschen Differentialgleichung folgt zunächst
mit einer Konstanten
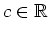 bis auf Ecken von
bis auf Ecken von
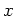 . Quadrieren wir diese Gleichung, so erhalten wir
und somit
mit
. Quadrieren wir diese Gleichung, so erhalten wir
und somit
mit
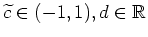 .
Mit dem Anfangswert
.
Mit dem Anfangswert
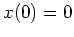 ergibt sich
ergibt sich
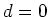 , d.h. die Extremalen
für
, d.h. die Extremalen
für
![$ \mbox{$t\in [0,1]$}$](img10.png) ,
,
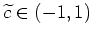 .
.
- Da der Integrand nicht von
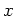 anhängt, folgt aus der Eulerschen Differentialgleichung
mit einer Konstanten
anhängt, folgt aus der Eulerschen Differentialgleichung
mit einer Konstanten
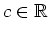 für alle
für alle
![$ \mbox{$t\in [1,2]$}$](img13.png) bis auf Ecken von
bis auf Ecken von
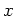 . Mit den Anfangswerten folgt daraus
. Mit den Anfangswerten folgt daraus
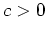 sowie
sowie
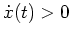 für
für
![$ \mbox{$t\in [1,2]$}$](img13.png) und wir erhalten
für
und wir erhalten
für
![$ \mbox{$t\in [1,2]$}$](img13.png) . Also ist
mit einer Konstanten
. Also ist
mit einer Konstanten
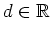 . Die Anfangswerte
. Die Anfangswerte
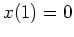 und
und
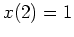 liefern schließlich
woraus sich sofort die Gleichung
ergibt. Durch zweimaliges Quadrieren dieser Gleichung erhalten wir mit der Bedingung
liefern schließlich
woraus sich sofort die Gleichung
ergibt. Durch zweimaliges Quadrieren dieser Gleichung erhalten wir mit der Bedingung
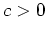 die Lösung
Die eindeutige Lösung des Problems ist also
für
die Lösung
Die eindeutige Lösung des Problems ist also
für
![$ \mbox{$t\in [1,2]$}$](img13.png) .
.
- Die Eulersche Differentialgleichung liefert
für
![$ \mbox{$t\in [-1,1]$}$](img26.png) bis auf Ecken von
bis auf Ecken von
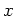 . Diese Funktion erfüllt jedoch nicht die Randbedingung
. Diese Funktion erfüllt jedoch nicht die Randbedingung
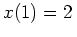 , also gibt es keine Extremale, die die Randwertbedingungen erfüllt.
, also gibt es keine Extremale, die die Randwertbedingungen erfüllt.
- Es sei
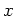 eine Extremale, also eine stetig differenzierbare Lösung der Eulerschen Differentialgleichung
Dann ist
eine Extremale, also eine stetig differenzierbare Lösung der Eulerschen Differentialgleichung
Dann ist
![$ \mbox{$x \in C^2[0,1]$}$](img29.png) und es gilt
Dies ist eine inhomogene lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten. Die allgemeine Lösung der
zugehörigen homogenen Gleichung ist gegeben durch
mit Konstanten
und es gilt
Dies ist eine inhomogene lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten. Die allgemeine Lösung der
zugehörigen homogenen Gleichung ist gegeben durch
mit Konstanten
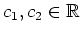 .
.
Wir bestimmen nun eine partikuläre Lösung der gegeben Differentialgleichung. Dabei wählen wir als Ansatzfunktion
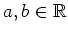 . Damit ist
d.h. eine partikuläre Lösung der inhomogenen Differentialgleichung ist gegeben durch
Folglich lautet die allgemeine Lösung der inhomogenen Differentialgleichung
mit Konstanten
. Damit ist
d.h. eine partikuläre Lösung der inhomogenen Differentialgleichung ist gegeben durch
Folglich lautet die allgemeine Lösung der inhomogenen Differentialgleichung
mit Konstanten
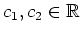 .
.
Im Hinblick auf die Anfangsbedingungen
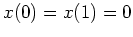 lösen wir das lineare Gleichungssystem
Die Lösung dieses Gleichungssystems lautet
lösen wir das lineare Gleichungssystem
Die Lösung dieses Gleichungssystems lautet
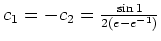 , so daß die eindeutige Lösung der Eulerschen Differentialgleichung, die die Randbedingungen erfüllt, durch
gegeben ist.
, so daß die eindeutige Lösung der Eulerschen Differentialgleichung, die die Randbedingungen erfüllt, durch
gegeben ist.
![$ \mbox{$\displaystyle
\frac{\dot x(t)}{\sqrt{1+\dot x(t)^2}}\,= c, \; t \in [0,1],
$}$](img1.png)
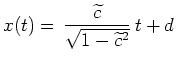
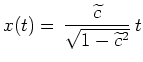
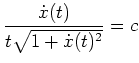
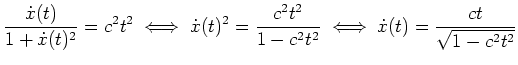
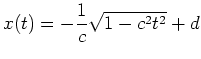
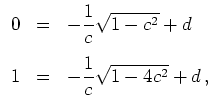
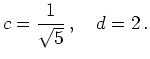
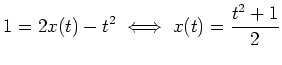
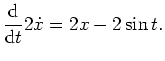
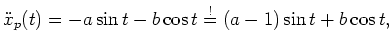
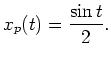
![$ \mbox{$\displaystyle
x(t) = c_1 e^{-t} + c_2 e^t + \frac{\sin t}{2}, \; t \in [0,1],
$}$](img37.png)
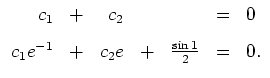
![$ \mbox{$\displaystyle
x(t) = \dfrac{\sin 1}{2 (e-e^{-1})} \, e^{-t} - \dfrac{\sin 1}{2 (e-e^{-1})} \, e^{t} + \frac{\sin t}{2}, \, t \in [0,1],
$}$](img41.png)
![$ \mbox{$\displaystyle
\frac{\dot x(t)}{\sqrt{1+\dot x(t)^2}}\,= c, \; t \in [0,1],
$}$](img1.png)
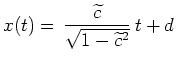
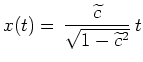
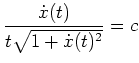
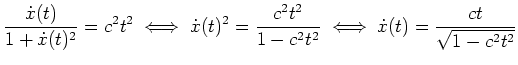
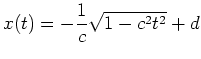
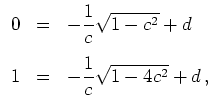
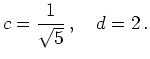
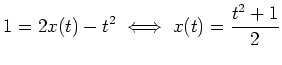
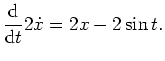
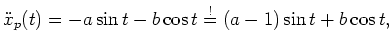
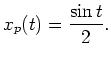
![$ \mbox{$\displaystyle
x(t) = c_1 e^{-t} + c_2 e^t + \frac{\sin t}{2}, \; t \in [0,1],
$}$](img37.png)
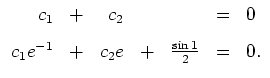
![$ \mbox{$\displaystyle
x(t) = \dfrac{\sin 1}{2 (e-e^{-1})} \, e^{-t} - \dfrac{\sin 1}{2 (e-e^{-1})} \, e^{t} + \frac{\sin t}{2}, \, t \in [0,1],
$}$](img41.png)